College Algebra
Tutorial 51: Systems of
Linear Equations
and Problem Solving
 Learning Objectives Learning Objectives
After completing this tutorial, you should be able to:
- Use Polya's four step process to solve various problems involving systems
of linear equations in both two and three variables.
|
 Introduction Introduction
Hey, lucky you, we have another tutorial on word problems. As
mentioned before, whether you like it or not, whether you are going to
be a mother, father, teacher, computer programmer, scientist, researcher,
business owner, coach, mathematician, manager, doctor, lawyer,
banker (the list can go on and on), problem solving is everywhere.
Some people think that you either can do it or you can't. Contrary
to that belief, it can be a learned trade. Even the best athletes
and musicians had some coaching along the way and lots of practice - that's
what it also takes to be good at problem solving.
The word problems in this section all involve setting up a system of
linear equations to help solve the problem. Basically, we are
combining the concepts from Tutorial
16: Formulas and Applications, Tutorial
49: Solving Systems of Linear Equations in Two Variables and Tutorial
50: Solving Systems of Linear Equations in Three Variables all
rolled up into one tutorial. We will be looking at different types
of word problems involving such ideas as distance, percentages, and something
we can all relate to MONEY!!! |
 Tutorial Tutorial
Polya's Four Step Process
for Problem Solving
(revisited)
|
This is the exact same process for problem solving that was introduced
in Tutorial 16: Formulas and Applications
The difference is in this tutorial we will be setting up a system of linear
equations as opposed to just working with one equation. |
Step 1: Understand
the problem. |
Sometimes the problem lies in understanding the problem.
If you are unclear as to what needs to be solved, then you are probably
going to get the wrong results. In order to show an understanding
of the problem you of course need to read the problem carefully.
Sounds simple enough, but some people jump the gun and try to start solving
the problem before they have read the whole problem. Once the problem
is read, you need to list out all the components and data that are involved.
This is where you will be assigning your variables. In the problems on this page, we will be letting
each unknown be a separate variable. So, if you have two
unknowns, you will have two variables, x and y.
If you have three unknowns, you will have three variables, x, y,
and z. |
Step 2: Devise
a plan (translate). |
When you devise a plan (translate), you come up with a way to
solve the problem. Setting up an equation, drawing a diagram, and
making a chart are all ways that you can go about solving your problem.
In this tutorial, we will be setting up equations for each problem.
In the problems on this page, we will be setting
up systems of linear equations. The number of equations need to match
the number of unknowns. For example, if you have two variables,
then you will need two equations. If you have three variables, then
you will need three equations. |
Step 3: Carry out
the plan (solve). |
Step 4: Look back (check
and interpret). |
You may be familiar with the expression don't look back. In problem
solving it is good to look back (check and interpret).. Basically,
check to see if you used all your information and that the answer makes
sense. If your answer does check out make sure that you write your
final answer with the correct labeling. |
 Example
1 Example
1: The sum of three numbers is 14. The
largest is 4 times the smallest, while the sum of the smallest and twice
the largest is 18. Find the numbers. |
Make sure that you read the question carefully several times.
Since we are looking for three numbers, we will let
x = the smallest number
y = middle number
z = the largest number
|
Since we have three unknowns, we need to build
a system with three equations.
Equation (1):
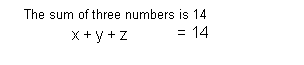
Equation (2):
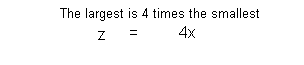
Equation (3):
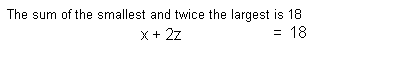
|
Putting the three equations together in a system we get:
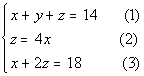
|
|
Simplify and put all three equations in the
form Ax + By + Cz = D if needed.
Equation (2) needs to be put in the correct form: |
|
*Inverse of add 4x is sub. 4x
|
Choose to eliminate any one of the variables
from any pair of equations.
Since y is already eliminated in equation
(4) and (3), it would be quickest and easiest to eliminate y.
We can use equation (4) as one equation with y eliminated: |
Eliminate the SAME variable chosen in step
2 from any other pair of equations, creating a system of two equations
and 2 unknowns.
We can use equation (3) as another equation with y eliminated: |
Solve the remaining system found in step 2
and 3.
Putting those two equations together we get: |
I'm going to choose to eliminate z.
Multiplying equation (4) by -2 and then adding that to equation (3)
we get: |
|
*Mult. both sides of eq. (4) by -2
*z's have opposite
coefficients
*z's dropped out |
|
*Inverse of mult. by 9 is div. by 9
|
Using equation (4) to plug 2 in for x and solving for z we get: |
|
*Equation (4)
*Plug in 2 for x
*Inverse of sub. 8 is add 8
|
Solve for the third variable.
Using equation (1) to plug in 2 for x and 8 for z and solving for y we get: |
|
*Equation (1)
*Plug in 2 for
x and 8 for z
*Inverse of add 10 is sub. 10
|
You will find that if you plug the ordered triple (2, 4, 8) into ALL
THREE equations of the original system, this is a solution to ALL
THREE of them.
Final Answer:
2 is the smallest number, 4 is the middle number and 8 is the largest
number. |
 Example
2 Example
2: How many gallons of 20% alcohol solution
and 50% alcohol solution must be mixed to get 9 gallons of 30% alcohol
solution? |
Make sure that you read the question carefully several times.
Since we are looking for two different amounts, we will let
x = the number of gallons of 20% alcohol
solution
y = the number of gallons of 50% alcohol
solution
|
Since we have two unknowns, we need to build
a system with two equations.
Equation (1):
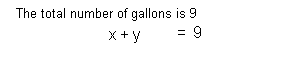
Equation (2):
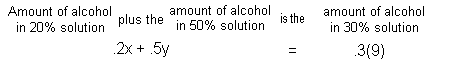
|
Putting the two equations together in a system we get:
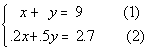
|
|
Simplify if needed.
We can simplify this by multiplying both sides of equation (2) by
10 and getting rid of the decimals: |
|
*Mult. both sides of eq. (2) by 10
|
|
Multiply one or both equations by a number
that will create opposite coefficients for either x or y if needed AND
add the equations.
If we multiply equation (1) by -2, then the x's
will have opposite coefficients.
Multiplying equations (1) by -2 and then adding
that to equation (3) we get: |
|
*Mult. both side of eq. (1) by -2
*x's have opposite
coefficients
*x's dropped out |
Solve for remaining variable.
Solving for y we get: |
|
*Inverse of mult. by 3 is divide by 3
|
Solve for second variable.
Using equation (1) to plug in 3 for y and solving for x we get: |
|
*Equation (1)
*Plug in 3 for y
*Inverse of add 3 is sub. 3
|
You will find that if you plug the ordered pair (6, 3) into BOTH equations
of the original system, that this is a solution to BOTH of them.
Final Answer:
6 gallons of 20% solution and 3 gallons of 50% solution |
 Example
3 Example
3: An airplane flying with the wind can cover
a certain distance in 2 hours. The return trip against the wind takes
2.5 hours. How fast is the plane and what is the speed of the air,
if the one-way distance is 600 miles? |
Make sure that you read the question carefully several times.
Since we are looking for two different rates, we will let
x = rate of the plane
y = the rate of the wind
Since this is a rate/distance problem, it might be good to organize
our information using the distance formula.
Keep in mind that the wind speed is affecting the overall speed.
When the plane is with the wind, it will be going faster. That
rate will be x + y.
When the plane is going against the wind, it will be going slower.
That rate will be x - y.
|
|
(Rate)
|
(Time)
|
= Distance
|
|
With wind
|
x + y
|
2
|
600
|
|
Against wind
|
x - y
|
2.5
|
600
|
|
Since we have two unknowns, we need to build
a system with two equations.
Equation (1):
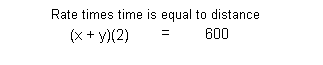
Equation (2):
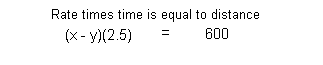
|
Putting the two equations together in a system we get:
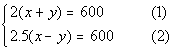
|
|
Simplify if needed.
We can simplify this by dividing both sides of equation (1) by 2
and equation (2) by 2.5 getting rid of the ( ) and decimals at the same
time: |
|
*Div. both side of eq. (1) by 2
*Div. both sides of eq. (2) by 2.5
|
|
Multiply one or both equations by a number
that will create opposite coefficients for either x or y if needed AND
add the equations.
Since we already have opposite coefficients
on y, we can go right into adding equations (3) and (4) together: |
|
*y's have opposite
coefficients
*y's dropped out |
Solve for remaining variable.
Solving for x we get: |
|
*Inverse of div. by 2 is mult. by 2
|
Solve for second variable.
Using equation (3) to plug in 270 for x and solving for y we get: |
|
*Equation (3)
*Plug in 270 for x
*Inverse of add 270 is sub. 270 |
You will find that if you plug the ordered pair (270, 30) into BOTH
equations of the original system, this is a solution to BOTH of them.
Final Answer:
The airplane speed is 270 mph and the air speed is 30 mph |
 Example
4 Example
4: Given the cost function C(x) and the revenue function R(x), find the number
of units x that must be sold to break even.
C(x) = 20x +
50000
R(x) = 25x |
Make sure that you read the question carefully several times.
We will let,
x = the number of units
C(x) = 20x + 50000
R(x) = 25x
This problem appears a little different because of the function notation.
Keep in mind that function notation translates to being y. |
In this problem, the two equations that we are
working with have already been given to us:
Cost function:
C(x) = 20x + 50000
Revenue function:
R(x) = 25x |
|
*Inverse of add 20x is sub. 20x
*Inverse of mult. by 5 is div. by 5
|
You will find that if you plug 10000 for x into BOTH equations that they BOTH come out to be 250000, which means this
is the break-even point.
Final Answer:
10000 units are needed to break-even |
 Practice Problems Practice Problems
These are practice problems to help bring you to the next level.
It will allow you to check and see if you have an understanding of these
types of problems. Math works just like anything
else, if you want to get good at it, then you need to practice it.
Even the best athletes and musicians had help along the way and lots of
practice, practice, practice, to get good at their sport or instrument.
In fact there is no such thing as too much practice.
To get the most out of these, you should work the problem out on
your own and then check your answer by clicking on the link for the answer/discussion
for that problem. At the link you will find the answer
as well as any steps that went into finding that answer. |
 Practice Problems 1a - 1c: Solve each word problem using systems of equations. Practice Problems 1a - 1c: Solve each word problem using systems of equations.
1a. The larger of two numbers is 5 more than twice the smaller.
If the smaller is subtracted from the larger, the result is 12. Find
the numbers.
(answer/discussion
to 1a) |
1b. It takes a boat 2 hours to travel 24 miles downstream and
3 hours to travel 18 miles upstream. What is the speed of the boat
in still water and of the current of the river?
(answer/discussion
to 1b) |
1c. A student has money in three accounts that pay 5%, 7%, and
8%, in annual interest. She has three times as much invested at 8%
as she does at 5%. If the total amount she has invested is $1600
and her interest for the year comes to $115, how much money does she have
in each account?
(answer/discussion
to 1c) |
 Need Extra Help on these Topics? Need Extra Help on these Topics?

Last revised on April 29, 2011 by Kim Seward.
All contents copyright (C) 2002 - 2011, WTAMU and Kim Seward. All rights reserved.
|
|


