College Algebra
Tutorial 16: Formulas and Applications

WTAMU > Virtual Math Lab > College Algebra

Learning Objectives

After completing this tutorial, you should be able to:

Translate an English phrase into an algebraic expression.
Use Polya's four step process to solve word problems.
Solve a formula for a given variable.

Introduction

Whether you like it or not, whether you are going to be a mother, father, teacher, computer programmer, scientist, researcher, business owner, coach, mathematician, manager, doctor, lawyer, banker (the list can go on and on), problem solving is everywhere. Some people think that you either can do it or you can't. Contrary to that belief, it can be a learned trade. Even the best athletes and musicians had some coaching along the way and lots of practice. That's also what it takes to be good at problem solving.

George Polya, known as the father of modern problem solving, did extensive studies and wrote numerous mathematical papers and three books about problem solving. I'm going to show you his method of problem solving to help step you through these problems.

Tutorial

Translating an
English Phrase Into an
Algebraic Expression

Sometimes, you find yourself having to write out your own algebraic expression based on the wording of a problem.

In that situation, you want to

read the problem carefully,
pick out key words and phrases and determine their equivalent mathematical meaning,
replace any unknowns with a variable, and
put it all together in an algebraic expression.

The following are some key words and phrases and their translations:

Addition: sum, plus, add to, more than, increased by, total

Subtraction: difference of, minus, subtracted from, less than, decreased by, less

Multiplication: product, times, multiply, twice, of

Division: quotient, divide, into, ratio

Example 1: Write the phrase as an algebraic expression: The sum of -5 and a number.

In this example, we are not evaluating an expression, but we are wanting to rewrite it as an algebraic expression.

It looks like the only reference to a mathematical operation is the word sum, so what operation will we have in this expression? If you said addition, you are correct!!!

The phrase 'a number' indicates that it is an unknown number - there was no specific value given to it. So we will replace the phrase 'a number' with the variable x. We want to let our variable represent any number that is unknown

Putting everything together, we can translate the given English phrase with the following algebraic expression:

The sum of -5 and a number

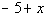
*'sum' = +
*'a number' = variable x

Let’s try another!

Example 2: Write the phrase as an algebraic expression: The product of 20 and a number.

Again, we are wanting to rewrite this as an algebraic expression, not evaluate it.

This time, the phrase that correlates with our operation is 'product' - so what operation will we be doing this time? If you said multiplication, you are right on.

Again, we have the phrase 'a number', which, again, is going to be replaced with a variable since we do not know what the number is.

Let’s see what we get for this answer:

The product of 20 and a number

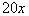
*'product' = multiplication
*'a number' = variable x

Example 3: Write the phrase as an algebraic expression: 7 less than twice a number.

First of all, we have the phrase 'less than' which mathematically translates as subtraction. You need to be careful with this phrase. It is very tempting to start off with 7 and put your subtraction sign after the 7. However, think about it, if you want 7 less than something, you are 7 below it. In order to be 7 below something you would have to subtract the 7!!! So you would not have 7 minus but minus 7 as PART of your expression.

The other part of the expression involves the phrase 'twice a number'. 'Twice' translates as two times a number and, as above, we will replace the phrase 'a number' with our variable x.

Putting this together we get:

7 less than twice a number

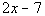
*'less than' = -
*'twice' = 2 times
*'a number' = variable x

Example 4: Write the phrase as an algebraic expression: The quotient of 9 and the difference of 8 and a number.

First of all, the term 'quotient' is going to be replaced with what mathematical operation? If you said division, you are right on the mark!!

Note how 9 immediately follows the phrase 'the quotient of', this means that 9 is going to be in the numerator. The phrase that immediately follows the word 'quotient' is going to be in the numerator of the fraction.

After the word ‘and', you have the phrase 'the difference of 8 and a number'. That is the second part of your quotient which means it will go in the denominator. And what operation will we have when we do write that difference down below? I hope you said subtraction.

Let’s see what we get when we put all of this together:

The quotient of 9 and the difference of 8 and a number.

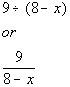
example 4a

*'quotient' = division
*'difference' = -
*'a number' = variable x

Polya's Four Steps to Problem Solving

As mentioned above, I use Polya’s four steps to problem solving to show students how to solve word problems. Just note that your math teacher or math book may word it a little differently, but you will see it all basically means the same thing.

If you follow these steps, it will help you become more successful in the world of problem solving.

Polya created his famous four-step process for problem solving, which is used all over to aid people in problem solving:

Step 1: Understand the problem.

Sometimes the problem lies in understanding the problem. If you are unclear as to what needs to be solved, then you are probably going to get the wrong results. In order to show an understanding of the problem, you, of course, need to read the problem carefully. Sounds simple enough, but some people jump the gun and try to start solving the problem before they have read the whole problem. Once the problem is read, you need to list all the components and data that are involved. This is where you will be assigning your variable.

Step 2: Devise a plan (translate).

When you devise a plan (translate), you come up with a way to solve the problem. Setting up an equation, drawing a diagram, and making a chart are all ways that you can go about solving your problem. In this tutorial, we will be setting up equations for each problem. You will translate them just like we did above.

Step 3: Carry out the plan (solve).

The next step, carry out the plan (solve), is big. This is where you solve the equation you came up with in your 'devise a plan' step. The equations in this tutorial will all be linear equations. If you need help solving them, by all means, go back to Tutorial 14: Linear Equations in One Variable and review that concept.

Step 4: Look back (check and interpret).

You may be familiar with the expression 'don't look back'. In problem solving it is good to look back (check and interpret). Basically, check to see if you used all your information and that the answer makes sense. If your answer does check out, make sure that you write your final answer with the correct labeling.

Numeric Word Problems

A lot of numeric types of word problems revolve around translating English statements into mathematical ones.

Just read and translate it left to right to set up your equation

Example 5: Three times the difference of a number and 4 is 8 more than that number. Find the number.

Step 1: Understand the problem.

Make sure that you read the question carefully several times.

Since we are looking for a number, we will let

x = a number

Step 2: Devise a plan (translate).

Step 3: Carry out the plan (solve).

*Remove ( ) by using dist. prop.

*Get all the x terms on one side

*Inv. of sub. 12 is add. 12

*Inv. of mult. by 2 is div. by 2

Step 4: Look back (check and interpret).

If you take three times the difference of 10 and 4, that is the same as 8 more than 10, so this does check.

FINAL ANSWER:

The number is 10.

Example 6: One number is 5 less than another number. If the sum of the two numbers is 205, find each number.

Step 1: Understand the problem.

Make sure that you read the question carefully several times.

We are looking for two numbers, and since we can write the one number in terms of another number, we will let

x = another number

one number is 5 less than another number:

x - 5 = one number

Step 2: Devise a plan (translate).

Step 3: Carry out the plan (solve).

*Combine like terms

*Inv. of sub. 5 is add. 5

*Inv. of mult. 2 is div. 2

Step 4: Look back (check and interpret).

If we add 105 and 100 (a number 5 less than 105) we do get 205.

FINAL ANSWER:

One number is 100.

Another number is 105.

Example 7: Last year, the star running back of the local football team made 6 more touchdowns than the star receiver. Together, they had 36 touchdowns. Determine the number of touchdowns for each player last year.

Step 1: Understand the problem.

Make sure that you read the question carefully several times.

We are looking for two numbers, and since we can write the number of touchdowns the running back made in terms of the number of touchdowns the receiver made we will let

x = the number of touchdowns the receiver made

The running back made 6 more touchdowns than the receiver:

x + 6 = number of touchdowns the running back made

Step 2: Devise a plan (translate).

Step 3: Carry out the plan (solve).

*Combine like terms

*Inv. of add. 6 is sub. 6

*Inv. of mult. by 2 is div. by 2

Step 4: Look back (check and interpret).

If we add 15 and 21 (a number 6 more than 15) we do get 36.

FINAL ANSWER:

The number of touchdowns the receiver made was 15.

The number of touchdowns the running back made was 21

Consecutive Integers

Consecutive integers are integers that follow one another in order.

For example, 5, 6, and 7 are three consecutive integers.

If we let x represent the first integer, how would we represent the second consecutive integer in terms of x? Well if we look at 5, 6, and 7 - note that 6 is one more than 5, the first integer.

In general, we could represent the second consecutive integer by x + 1. And what about the third consecutive integer.

Well, note how 7 is 2 more than 5. In general, we could represent the third consecutive integer as x + 2.

Consecutive EVEN integers are even integers that follow one another in order.

For example, 4, 6, and 8 are three consecutive even integers.

If we let x represent the first EVEN integer, how would we represent the second consecutive even integer in terms of x? Note that 6 is two more than 4, the first even integer.

In general, we could represent the second consecutive EVEN integer by x + 2.

And what about the third consecutive even integer? Well, note how 8 is 4 more than 4. In general, we could represent the third consecutive EVEN integer as x + 4.

Consecutive ODD integers are odd integers that follow one another in order.

For example, 5, 7, and 9 are three consecutive odd integers.

If we let x represent the first ODD integer, how would we represent the second consecutive odd integer in terms of x? Note that 7 is two more than 5, the first odd integer.

In general, we could represent the second consecutive ODD integer by x + 2.

And what about the third consecutive odd integer? Well, note how 9 is 4 more than 5. In general, we could represent the third consecutive ODD integer as x + 4.

Note that a common misconception is that because we want an odd number that we should not be adding a 2 which is an even number. Keep in mind that x is representing an ODD number and that the next odd number is 2 away, just like 7 is 2 away from 5, so we need to add 2 to the first odd number to get to the second consecutive odd number.

Example 8: The sum of 4 consecutive integers is 406. Find the integers.

Step 1: Understand the problem.

Make sure that you read the question carefully several times.

We are looking for 4 consecutive integers, we will let

x = 1st consecutive integer

x + 1 = 2nd consecutive integer

x + 2 = 3rd consecutive integer

x + 3 = 4th consecutive integer

Step 2: Devise a plan (translate).

Step 3: Carry out the plan (solve).

*Combine like terms
*Inv. of add. 6 is sub. 6

*Inv. of mult. by 4 is div. by 4

Step 4: Look back (check and interpret).

The sum of 100, 101, 102, and 103 does check to be 406.

FINAL ANSWER:

The three consecutive integers are 100, 101, 102, and 103.

Example 9: The ages of 3 sisters are 3 consecutive odd integers. If the sum of the 1st odd integer, 3 times the 2nd odd integer, and twice the 3rd odd integer is 68, find each age.

Step 1: Understand the problem.

Make sure that you read the question carefully several times.

We are looking for 3 ODD consecutive integers, we will let

x = 1st consecutive odd integer

x + 2 = 2nd consecutive odd integer

x + 4 = 3rd consecutive odd integer

Step 2: Devise a plan (translate).

Step 3: Carry out the plan (solve).

*Remove ( ) by using dist. prop.
*Combine like terms

*Inv. of add. 14 is sub. 14

*Inv. of mult. by 6 is div. by 6

Step 4: Look back (check and interpret).

If we take the sum of 9, three times 11, and twice 13, we do get 68.

FINAL ANSWER:

The ages of the three sisters are 9, 11 and 13.

Rectangle Problem

The following formula will come in handy for solving example 10:

Perimeter of a rectangle = 2(length) + 2(width)

Example 10: In a blueprint of a rectangular room, the length is 2 inches less than 4 times the width. Find the dimensions if the perimeter is 46 inches.

Step 1: Understand the problem.

Make sure that you read the question carefully several times.

We are looking for the length and width of the rectangle. Since length can be written in terms of width, we will let

w = width

length is 2 inches less than 4 times the width:

4w - 2 = length

Step 2: Devise a plan (translate).

Step 3: Carry out the plan (solve).

*Remove ( ) by using dist. prop.
*Combine like terms

*Inv. of sub. 4 is add. 4

*Inv. of mult. by 10 is div. by 10

Step 4: Look back (check and interpret).

If the width is 5, then the length, which is 2 inches less than 4 times the width, would have to be 18. The perimeter of a rectangle with width of 5 inches and length of 18 inches does come out to be 46 inches.

FINAL ANSWER:

Width is 5 inches.

Length is 18 inches.

Percent Problems

Whenever you are working with a percent problem, you need to make sure you write your percent in decimal form. You do this by moving the decimal place of the percent two to the left. For example, 32% in decimal form is .32.

When you are wanting to find the percentage of some number, remember that ‘of ’ represents multiplication - so you would multiply the percent (in decimal form) times the number you are taking the percent of.

Example 11: Find 73% of 225.

Step 1: Understand the problem.

Make sure that you read the question carefully several times.

We are looking for a number that is 73% of 225, we will let

x = the value we are looking for

Step 2: Devise a plan (translate).

Step 3: Carry out the plan (solve).

*Multiply

Step 4: Look back (check and interpret).

164.25 is 73% of 225.

FINAL ANSWER:

The number is 164.25.

Example 12: A math class has 45 students. Approximately 60% are females. How many students are females?

Step 1: Understand the problem.

Make sure that you read the question carefully several times.

We are looking for how many students are females, we will let

x = number of female students

Step 2: Devise a plan (translate).

Step 3: Carry out the plan (solve).

*Multiply

Step 4: Look back (check and interpret).

27 is 60% of 45.

FINAL ANSWER:

27 students are female.

Example 13: You purchased a new computer monitor at a local electronics store for $216.50, which included tax. If the tax rate is 8.25%, find the price of the monitor before they added the tax.

Step 1: Understand the problem.

Make sure that you read the question carefully several times.

We are looking for the price of the computer monitor before they added the tax, we will let

x = price of the computer monitor before tax was added.

Step 2: Devise a plan (translate).

Step 3: Carry out the plan (solve).

*Combine like terms

*Inv of mult. 1.0825 is div. by 1.0825

Step 4: Look back (check and interpret).

If you add on 8.25% tax to 200, you would get 216.50.

FINAL ANSWER:

The original price is $200.

Formulas

A formula is an equation that involves two or more variables that have a specific relationship with each other.

Solving a Formula for a Specified Variable

Basically, you want to get the variable you are solving for alone on one side and everything else on the other side (including variables you are not solving for) using INVERSE operations.

Even though there is more than one variable in a formula, you solve for a specific variable using the exact same steps that you do with an equation in one variable, as shown in Tutorial 14: Linear Equations in One Variable.

It is really easy to get overwhelmed when there is more than one variable involved. Sometimes your head feels like it is spinning when you see all of those variables. Isn’t math suppose to be about numbers? Well, just remember that a variable represents a number. So if you need to move it to the other side of the equation you use inverse operations, just like you would do with a number.

Example 14: Solve the equation for l.

Do you recognize this formula?
This happens to be the formula for the volume of a rectangular solid, where V = volume, l = length, w = width, and h = height.

In this problem, we need to solve for l. This means we need to get l on one side and EVERYTHING ELSE on the other side using inverse operations.

Let’s solve this formula for l:

*Inverse of mult. by wh is div. by wh

*Formula solved for l

Example 15: Solve the equation P = 2L + 2W for W.

Do you recognize this formula?
This happens to be the formula for the perimeter of a rectangle, where P = perimeter, L = length, and W = width.

In this problem, we need to solve for W. This means we need to get W on one side and EVERYTHING ELSE on the other side using inverse operations.

Let’s solve this formula for W:

*Inverse of add 2L is sub. 2L

*Inverse of mult. by 2 is div. by 2

*Formula solved for W

Practice Problems

These are practice problems to help bring you to the next level. It will allow you to check and see if you have an understanding of these types of problems. Math works just like anything else, if you want to get good at it, then you need to practice it. Even the best athletes and musicians had help along the way and lots of practice, practice, practice, to get good at their sport or instrument. In fact there is no such thing as too much practice.

To get the most out of these, you should work the problem out on your own and then check your answer by clicking on the link for the answer/discussion for that problem. At the link you will find the answer as well as any steps that went into finding that answer.

1a. In last night’s basketball game, Sally scored 9 less than twice what Lucy scored. The sum of their scores is 27. How many points did Sally and Lucy make individually?
(answer/discussion to 1a)

1b. The heights in inches of three basketball players are 3 consecutive integers. If the sum of twice the 1st, 3 times the 2nd, and the 3rd is 437, what are the three heights.
(answer/discussion to 1b)

1c. A rectangular floor has a perimeter of 54 feet. If the length is 3 more than the width, what are the dimensions of the floor?
(answer/discussion to 1c)

1d. The original price of a CD player was marked down 15% and is now $127.50, how much was the original price?
(answer/discussion to 1d)

2a.

for T
(answer/discussion to 2a)

2b.

for m
(answer/discussion to 2b)

Need Extra Help on these Topics?

The following are webpages that can assist you in the topics that were covered on this page:

http://www.wtamu.edu/academic/anns/mps/math/mathlab/int_algebra/int_alg_tut8_probsol.htm
This website helps you with basic problem solving.

http://www.wtamu.edu/academic/anns/mps/math/mathlab/int_algebra/int_alg_tut9_form.htm
This webpage helps you with solving a formula for a given variable.

http://www.purplemath.com/modules/translat.htm
This webpage gives you the basics of problem solving and helps you with translating English into math.

http://www.purplemath.com/modules/numbprob.htm
This webpage helps you with numeric and consecutive integer problems.

http://www.purplemath.com/modules/percntof.htm
This webpage helps you with percent problems.

http://www.purplemath.com/modules/ageprobs.htm
This webpage goes through examples of age problems, which are like the numeric problems found on this page.

http://www.purplemath.com/modules/solvelit.htm
This webpage helps you with solving formulas for a specified variable.

Go to Get Help Outside the Classroom found in Tutorial 1: How to Succeed in a Math Class for some more suggestions.

WTAMU > Virtual Math Lab > College Algebra

Videos at this site were created and produced by Kim Seward and Virginia Williams Trice.
Last revised on Dec. 15, 2009 by Kim Seward.
All contents copyright (C) 2002 - 2010, WTAMU and Kim Seward. All rights reserved.