

![]()
What do you think it is?
Let's find out if you are right:
![]()
Since 9 squared is 81, 9 is the square root of 81.
Note that we are only interested in the principal root and since 81
is positive and there is not a sign in front of the radical, our answer
is positive 9. If there had been a negative in front of the radical
our answer would have been -9.
![]()
What do you think it is?
Let's find out if you are right:
![]()
Since -3 cubed is -27, -3 is the cube root of -27.
![]()
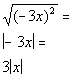
Since the root number and the exponent inside are equal and are the even number 2, we need to put an absolute value around x for our answer.
The reason for the absolute value is that we do not know if x is positive or negative. So if we put x as
our answer and it was negative, it would not be a true statement.
![]()
What do you think it is?
Let's find out if you are right:
Since there is no such real number that when we square it we get -4,
then the answer is not a real number.
![]()
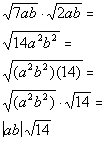
Since we cannot take the square root of 14 and 14 does not have any
factors we can take the square root of, this is as simplified as it gets.
![]()
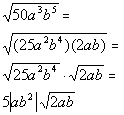
![]()
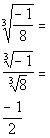
*The cube root of -1 is -1 and the cube root
of 8 is 2
![]()
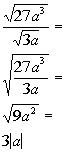
*Simplify the fraction
*The square root of 9 a squared is 3|a|
![]()
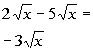
![]()
Can you think of what that factor is?
Let's see what we get when we simplify the first radical:
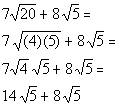
*Square root of 4 is 2
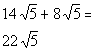
![]()
Square roots are nice to work with in this type of problem because if the radicand is not a perfect square to begin with, we just have to multiply it by itself and then we have a perfect square.
So in this case we can accomplish this by multiplying top and bottom
by the square root of 7:
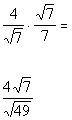
*Den. now has a perfect square under sq. root
AND
![]()
So what would the conjugate of our denominator be?
It looks like the conjugate is ![]() .
.
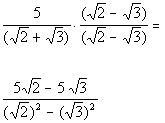
*Use distributive prop. to multiply the numerators
*In general, product of conjugates is ![]()
AND
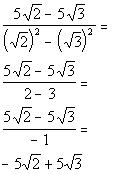
*Square root of 2 squared is 2 and the square
root of 3 squared is 3
*Divide BOTH terms of num. by -1
Last revised on Dec. 6, 2009 by Kim Seward.
All contents copyright (C) 2002 - 2010, WTAMU and Kim Seward. All rights reserved.