College Algebra
Answer/Discussion to Practice Problems
Tutorial 40: Graphs of Rational Functions
Answer/Discussion
to 1a
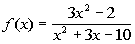
Our restriction here is that the denominator of a
fraction can never
be equal to 0. So to find our domain, we want to set the
denominator
equal to 0 and restrict those values.
*The
den. cannot equal to 0
*Factoring to help "solve"
*2 and -5 are restricted values
Our domain is all real
numbers except 2 and -5, because 2 and -5 both make the
denominator equal to 0, which would not give us a real number answer
for our function.
Answer/Discussion
to 2a
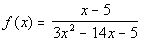
Reducing the rational
function to lowest terms we get:
*Factor
*Cancel the common factor of x - 5
Vertical Asymptote:
So now
we want to find where the denominator
is equal to 0:
*Set den = 0
There is one vertical asymptote: x = -1/3.
Horizontal Asymptote:
So now we want to
compare the degrees of the numerator and the denominator.
What
is the degree of the numerator that is left? If you said
0, you are
correct. The leading term is the constant 1 and its degree is 0.
What
is the degree of the denominator that is left? If you said
1, you are
correct. The leading term is
x and its
degree is 1.
If you need a review of finding the degree of a polynomial, feel free
to go to
Tutorial 6: Polynomials.
Since the degree of the numerator is 1 is less than the degree of the
denominator, then there is a
horizontal asymptote at y = 0.
Answer/Discussion
to 2b
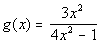
This rational function
is already in lowest terms:
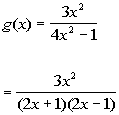
Vertical Asymptote:
So now
we want to find where the denominator
is equal to 0:
*Set den = 0
There are two vertical asymptotes: x = -1/2 and 1/2.
Horizontal Asymptote:
So now we want to
compare the degrees of the numerator and the denominator.
What
is the degree of the numerator? If you said 2, you are
correct. The leading term is the constant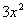
and its degree is 2.
What
is the degree of the denominator? If you said 2, you are
correct. The leading term is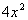
and its
degree is 2.
If you need a review of finding the degree of a polynomial, feel free
to go to
Tutorial 6: Polynomials.
Since the degree of the
numerator is equal to the degree of the denominator, then there is
a horizontal asymptote at
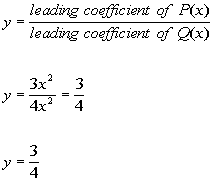
Answer/Discussion
to 3a
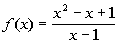
Note that this rational function is already reduced
down.
Applying long
division to this problem we get:
The answer to the long division would be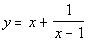
.
The equation for the slant
asymptote is the quotient part of the answer which would be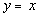 
.
Answer/Discussion
to 4a
*Factor
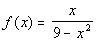
This function cannot be reduced any further. This
means that there will be no open holes on this graph.
Vertical Asymptote:
So now
we want to find where the denominator
is equal to 0:
*Set den = 0
*Set 1st factor = 0
*Set 2nd factor = 0
There are two vertical asymptotes: x = -3 and x = 3.
Horizontal Asymptote:
So now we want to
compare the degrees of the numerator and the denominator.
What
is the degree of the numerator? If you said 1, you are
correct. The leading term is
x and its degree is 1.
What
is the degree of the denominator? If you said 2, you are
correct. The leading term is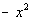
and its
degree is 2.
If you need a review of finding the degree of a polynomial, feel free
to go to
Tutorial 6: Polynomials.
Since the degree of the numerator is 1 is less than the degree of the
denominator, then there is a
horizontal asymptote at y = 0.
Slant Asymptote:
Since the degree of the numerator is NOT
one degree higher than the degree of the denominator, there is not
slant asymptote.
x-intercept:
What value are we going to use for y? You are correct if
you said 0.
*Plug in 0 for y
*x-intercept at 0
There is an x-intercept at (0, 0).
y-intercept:
What value are we going to use for x? You are correct if
you said 0.
*Plug in 0 for x
*y-intercept at 0
There is an y-intercept at (0, 0).
Note how the vertical asymptotes sections the graph
into
three parts. I’m going to plug in two x values that are to the left
of x = -3, two in
between x = -3 and x = 3,
and two
that are to the right of x = 3.
Plugging in -5 for x we get:
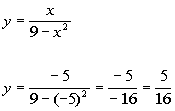(-5, 5/16)
Plugging in -4 for x we get:
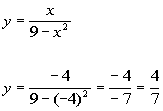(-4, 4/7)
Plugging in -1 for x we get:
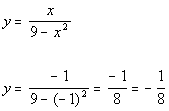(-1, -1/8)
Plugging in 1 for x we get:
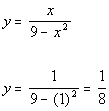(1, 1/8)
Plugging in 4 for x we get:
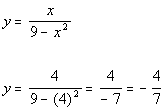(4, -4/7)
Plugging in 5 for x we get:
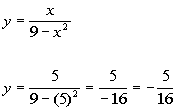(5, -5/16)
Step 6: Draw curves through the points,
approaching the asymptotes.
Answer/Discussion
to 4b
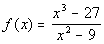
*Factor
*Cancel the common factor of x - 3
The factor of x - 3 canceled out and there were no other factors of x - 3 left in the denominator. This means there is an open hole on
the graph at x = 3.
x = 3:
*Plug in a 3 for x
There is an open hole
at (3, 9/2).
Vertical Asymptote:
So now
we want to find where the new
denominator is equal to 0:
*Set den. = 0
There is one vertical asymptote: x = -3.
Horizontal Asymptote:
Since the degree of the
numerator is one degree higher than the degree of the denominator,
there is a slant asymptote and no horizontal asymptote.
Slant Asymptote:
Applying long
division to this problem we get:
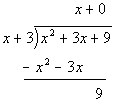
The answer to the long division would be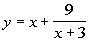
.
The equation for the slant
asymptote is the quotient part of the answer which would be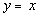 
.
x-intercept:
What value are we going to use for y? You are correct if
you said 0.
*Plug in 0 for y
*Mult. both side by the LCD (x + 3)
*Does NOT Factor
There are no real
number solutions to this equation, so there are no x-intercepts.
y-intercept:
What value are we going to use for x? You are correct if
you said 0.
*Plug in 0 for x
*y-intercept of 3
The y-intercept is (0, 3).
Note how the
vertical asymptote sections the graph into two parts. I’m going
to
plug in two x values that are to the left of x = -3 and two x values that are to the right of x = -3 .
Plugging in -5 for x we get:
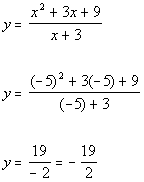(-5, -19/2)
Plugging in -4 for x we get:
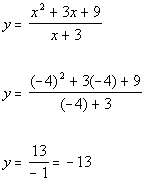(-4, -13)
Plugging in -2 for x we get:
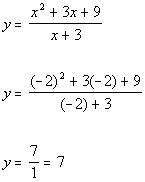(-2, 7)
Plugging in -1 for x we get:
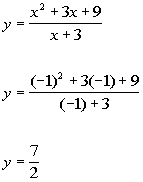(-1, 7/2)
Step 6: Draw
curves through the points, approaching the asymptotes.
Last revised on March 17, 2011 by Kim Seward.
All contents copyright (C) 2002 - 2011, WTAMU and Kim Seward. All rights reserved.
, the function is
neither even nor odd. 
