---

 

Answer/Discussion to 1a

 

Step 1: Determine the graph's end behavior.

 

Use the Leading Coefficient Test, described above, to find if the graph rises or falls to the left and to the right. Do you think that the graph rises or falls to the left and to the right? Since the degree of the polynomial, 4,  is even and the leading coefficient, -3, is negative, then the graph of the given polynomial falls to the left and falls to the right.

 

Step 2: Find the x-intercepts or zeros of the function.

 

*Factor out a GCF *Factor a Perfect Square Trinomial

 

First Factor:

 

*Setting the 1st factor = 0 *Solve for x *x = 0 is a zero

 

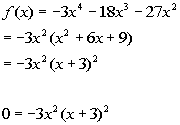
Since the exponent on this factor is 2, then the multiplicity for the zero x = 0 is 2.   Since the multiplicity is 2, which is even, then the graph touches the x-axis and turns around at the zero x = 0.

 

Second Factor:

 

*Setting the 2nd factor = 0 *Solve for x *x = -3 is a zero

 

Since the exponent on this factor is 2, then the multiplicity for the zero x = -3 is 2.   Since the multiplicity is 2, which is even, then the graph touches the x-axis and turns around at the zero x = -3.

 

Step 3: Find the y-intercept of the function.

 

Letting x = 0 we get:

 

*Plug in 0 for x

 

The y-intercept is (0, 0).

 

Step 4: Determine if there is any symmetry.

 

y-axis symmetry:

 

*Plug in -x for x

 

It is not symmetric about the y-axis.

 

Origin symmetry:

 

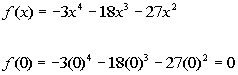
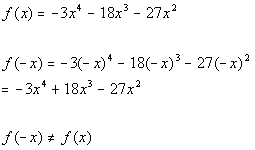
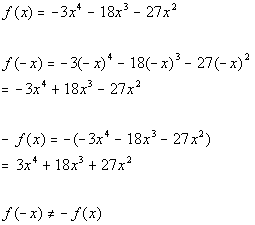
*Plug in -x for x   *Take the opposite of f(x)

 

It is not symmetric about the origin.

 

Step 5: Find the number of maximum turning points.

 

Since the degree of the function is 4, then there is at most 4 - 1 = 3 turning points.

 

Step 6: Find extra points, if needed.

 

To get a more accurate curve, lets find some points that are in between the points we found in steps 2 and 3:

 

x		(x, y)
-2		(-2, -12)
-1		(-1, -12)

 

Step 7: Draw the graph.

 
 

(return to problem 1a)

 

Answer/Discussion to 1b

 

Step 1: Determine the graph's end behavior.

 

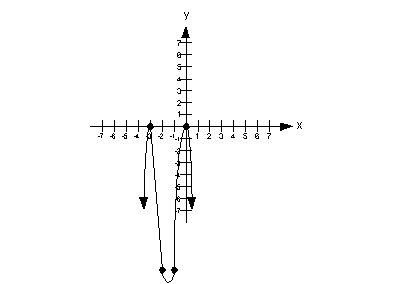
Use the Leading Coefficient Test, described above, to find if the graph rises or falls to the left and to the right. Do you think that the graph rises or falls to the left and to the right? Since the degree of the polynomial, 3, is odd and the leading coefficient, 1, is positive, the graph of the given polynomial falls to the left and rises to the right.

 

Step 2: Find the x-intercepts or zeros of the function.

 

*Factor out a GCF

 

First Factor:

 

*Setting the 1st factor = 0 *Solve for x *x = 0 is a zero

 

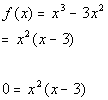
Since the exponent on this factor is 2, then the multiplicity for the zero x = 0 is 2.   Since the multiplicity is 2, which is even, then the graph touches the x-axis and turns around at the zero x = 0.

 

Second Factor:

 

*Setting the 2nd factor = 0 *Solve for x *x = 3 is a zero

 

Since the exponent on this factor is 1, then the multiplicity for the zero x = 3 is 1.   Since the multiplicity is 1, which is odd, then the graph crosses the x-axis at the zero x = 3.

 

Step 3: Find the y-intercept of the function.

 

Letting x = 0 we get:

 

*Plug in 0 for x

 

The y-intercept is (0, 0).

 

Step 4: Determine if there is any symmetry.

 

y-axis symmetry:

 

*Plug in -x for x

 

It is not symmetric about the y-axis.

 

Origin symmetry:

 

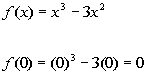
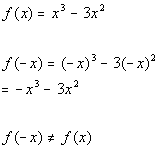
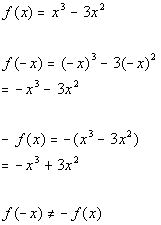
*Plug in -x for x     *Take the opposite of f(x)

 

It is not symmetric about the origin.

 

Step 5: Find the number of maximum turning points.

 

Since the degree of the function is 3, then there is at most 3 - 1 = 2 turning points.

 

Step 6: Find extra points, if needed.

 

To get a more accurate curve, lets find some points that are in between the points we found in steps 2 and 3:

 

x		(x, y)
1		(1, -2)
2		(2, -4)

 

Step 7: Draw the graph.

 
 

(return to problem 1b)

 

---

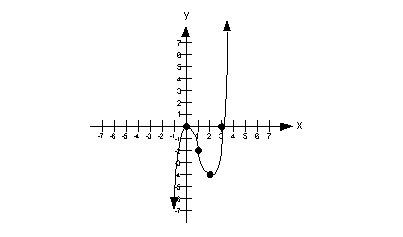
Last revised on March 14, 2012 by Kim Seward.
All contents copyright (C) 2002 - 2012, WTAMU and Kim Seward. All rights reserved.