

Slope = ½ and passes through the origin.
Do you know what the ordered pair for the origin is? If you said (0, 0) you are right on!!! That is the point that we will be using to plug into our equation.
Looks like we have all the information we need. We are ready to put our equation together.
Point/Slope Form:
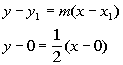
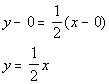
Passing through (-2, 4) and (-1, -1).
We have more than enough points. However, what about the slope? Does this mean we can't work out the problem? You are not going to get off that easily. We do have a way of finding the slope. Tutorial 25: The Slope of a Line shows us how we can get the slope given two points.
Let's find that slope:
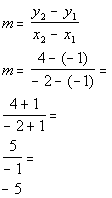
*Plug in values
*Simplify
Now we want to put the slope and one point into the point/slope equation. Note that you can use either point to plug in as long as it is a point that the line passes through. I chose to plug in the point (-2, 4).
Point/Slope Form:
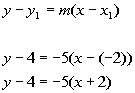
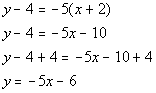
*Slope/intercept form of the line
x-intercept = -5 and y-intercept
= -2.
Do you know what the ordered pair is going to be for the x-intercept? What about the y-intercept?
Above, we leaned that an x-intercept is where the line crosses the x-axis. That means y's value is always 0. So the ordered pair for our x-intercept is (-5. 0).
Above, we learned that an y-intercept is where the line crosses the y-axis.
That means x's value is always 0. So
the ordered pair for our y-intercept is (0,
-2).
We have more than enough points. However, what about the slope? Does this mean we can't work out the problem? You are not going to get off that easily. We do have a way of finding the slope. Tutorial 25: The Slope of a Line shows us how we can get the slope given two points.
Let's find that slope:
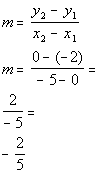
*Plug in values
*Simplify
We want to put the slope and one point into the point/slope equation. Note that you can use either point to plug in as long as it is a point that the line passes through. I chose to plug in the point (-5, 0).
Point/Slope Form:
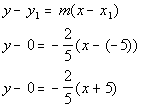
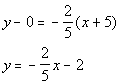
*Slope/intercept form of the line
Last revised on Feb. 6, 2010 by Kim Seward.
All contents copyright (C) 2002 - 2010, WTAMU and Kim Seward. All rights reserved.