College Algebra
Tutorial 25: Slope of a Line
 Learning Objectives Learning Objectives
After completing this tutorial, you should be able to:
- Know when a line rises, falls, is horizontal or is
vertical.
- Find the slope given two points on the line.
|
 Introduction Introduction
In this tutorial we will explore the slope of the
line. Basically,
the slope of the line measures the steepness of the line. We will
start with some visuals to help you understand what the slope of a
straight
line tells us about the line. Next, we will practice finding the
slope given two points on the line. Let's see what you can do
with
slopes. |
 Tutorial Tutorial
The slope of a line measures the steepness of the
line.
Most of you are probably familiar with associating slope
with "rise
over run".
Rise means how many units you move up or
down from point to
point. On the graph that would be a change in the y values.
Run means how far left or right you move
from point to point.
On the graph, that would mean a change of x values. |
Here are some visuals to help you with this
definition:
Positive Slope:
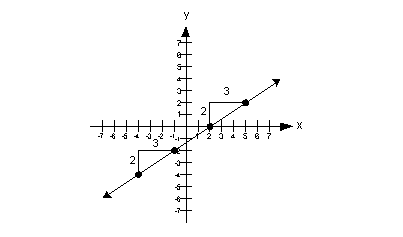
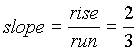
Note that when a line has a positive slope it rises
up left to right. |
| Negative Slope:
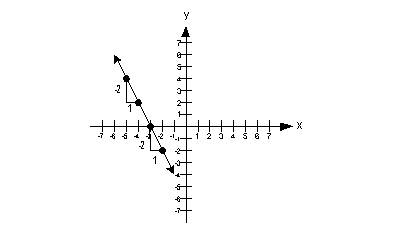
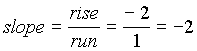
Note that when a line has a negative slope it falls
left to right. |
| Zero Slope:
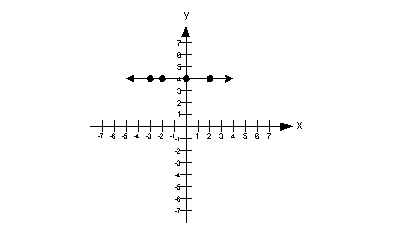
slope = 0
Note that when a line is horizontal the slope is 0. |
| Undefined Slope:
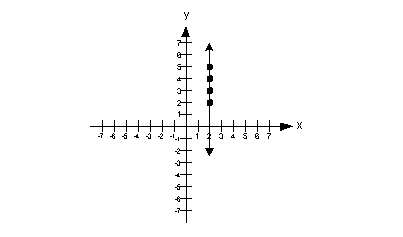
slope = undefined
Note that when the line is vertical the slope is
undefined. |
|
Slope Formula Given Two Points
Given two points 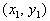 and and 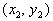
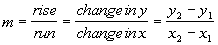
|
The subscripts just indicate that these are two
different points.
It doesn't matter which one you call point 1 and which one you call
point
2 as long as you are consistent throughout that problem.
Note that we use the letter m to represent
slope.
 Example
1: Find the slope of the straight line that passes through
(7,
5) and (5, 1) or state that the slope is undefined. Then indicate
if the line through the points rises (left to right), falls (left to
right),
is horizontal, or is vertical. Example
1: Find the slope of the straight line that passes through
(7,
5) and (5, 1) or state that the slope is undefined. Then indicate
if the line through the points rises (left to right), falls (left to
right),
is horizontal, or is vertical.
 View a video of this example View a video of this example
|
|
*Plug in x and y values into slope formula
*Simplify
|
The slope of the line is 2.
Since the slope is positive, the line would rise
(left to right). |
 Example
2 Example
2: Find the slope of the straight line that passes through
(1,
-4) and (-1, 3) or state that the slope is undefined. Then
indicate
if the line through the points rises (left to right), falls (left to
right),
is horizontal, or is vertical.
 View a video of this example View a video of this example
|
|
*Plug in x and y values into slope formula
*Simplify
|
Make sure that you are careful
when one of
your values is negative and you have to subtract it as we did in line
2.
1 - (-1) is not the same as 1 - 1.
The slope of the line is -7/2.
Since the slope is negative, the line would fall
(left to right). |
 Example
3 Example
3: Find the slope of the straight line that passes through
(4,
1) and (-2, 1) or state that the slope is undefined. Then
indicate
if the line through the points rises (left to right), falls (left to
right),
is horizontal, or is vertical.
 View a video of this example View a video of this example
|
|
*Plug in x and y values into slope formula
*Simplify
|
Make sure that you are careful
when one of
your values is negative and you have to subtract it as we did in line
2.
4 - (-2) is not the same as 4 - 2.
The slope of the line is 0.
Since the slope is zero, the line would be horizontal. |
 Example
4 Example
4: Find the slope of the straight line that passes through
(-2,
3) and (-2, 5) or state that the slope is undefined. Then
indicate
if the line through the points rises (left to right), falls (left to
right),
is horizontal, or is vertical.
 View a video of this example View a video of this example
|
|
*Plug in x and y values into slope formula
*Simplify
|
Make sure that you are careful
when one of
your values is negative and you have to subtract it as we did in line
2.
-2 - (-2) is not the same as -2 - 2.
The slope of the line is undefined.
Since the slope is undefined, the line would be
vertical. |
 Practice Problems Practice Problems
These are practice problems to help bring you to the next level.
It will allow you to check and see if you have an understanding of these
types of problems. Math works just like anything
else, if you want to get good at it, then you need to practice it.
Even the best athletes and musicians had help along the way and lots of
practice, practice, practice, to get good at their sport or instrument.
In fact there is no such thing as too much practice. To get the most out of these, you should work the problem out on
your own and then check your answer by clicking on the link for the answer/discussion
for that problem. At the link you will find the answer
as well as any steps that went into finding that answer. |
 Practice
Problems 1a - 1d: Find the slope of the straight line
that passes through
the given points or state that the slope is undefined. Then
indicate
if the line through the points rises (left to right), falls (left to
right),
is horizontal, or is vertical. Practice
Problems 1a - 1d: Find the slope of the straight line
that passes through
the given points or state that the slope is undefined. Then
indicate
if the line through the points rises (left to right), falls (left to
right),
is horizontal, or is vertical.
 Need Extra Help on these Topics? Need Extra Help on these Topics?

Videos at this site were created and produced by Kim Seward and Virginia Williams Trice.
Last revised on Jan. 16, 2010 by Kim Seward.
All contents copyright (C) 2002 - 2010, WTAMU and Kim Seward. All rights reserved.
|
|


