

![]()
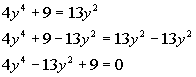
*Equation in standard form
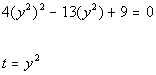
*When in stand. form, let t = the expression following b.
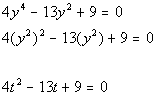
*Substitute t in
for y squared
I'm going to factor it to solve it.
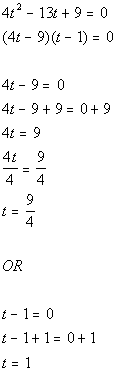
*Use Zero-Product Principle
*Set 1st factor = 0 and solve
*Set 2nd factor = 0 and solve
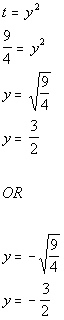
*First solution
*Second solution
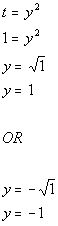
*First solution
*Second solution
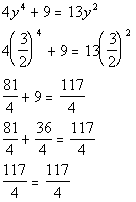
*True statement
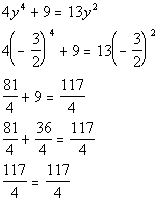
*True statement
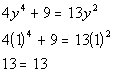
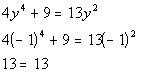
![]()
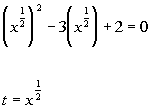
*When in stand. form, let t = the expression following b.
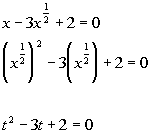
*Substitute t in
for x to the 1/2 power
I'm going to factor it to solve it.
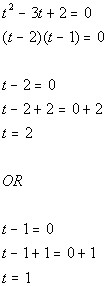
*Use Zero-Product Principle
*Set 1st factor = 0 and solve
*Set 2nd factor = 0 and solve
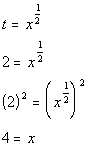
*Inverse of taking it to the 1/3 power is
raising it to the 3rd power
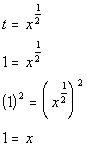
*Inverse of taking it to the 1/2 power is
raising it to the 2nd power
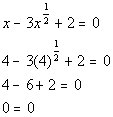
*True statement
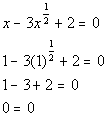
*True statement
![]()
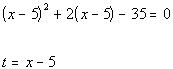
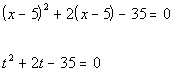
*Substitute t in
for x minus 5
I'm going to factor it to solve it.
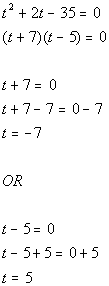
*Use Zero-Product Principle
*Set 1st factor = 0 and solve
*Set 2nd factor = 0 and solve
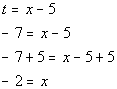
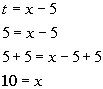
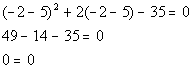
*True statement
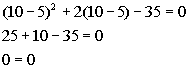
*True statement
Last revised on Dec. 16, 2009 by Kim Seward.
All contents copyright (C) 2002 - 2010, WTAMU and Kim Seward.
All rights reserved.