WTAMU > Virtual Math Lab > College Algebra > Tutorial 14: Linear Equations in One Variable
 Answer/Discussion
to 1a
|
 |
*Inverse of add. 3 is sub 3 from both sides
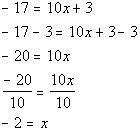
*Inverse of mult. by 10 is div. both sides
by 10
|
| If you put -2 back in for x in the original
problem you will see that -2 is the solution we are looking for. |
| Answer/Discussion
to 1b
|
 |
*Get all x terms
on one side
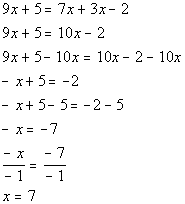
*Inverse of add. 5 is sub. 5
*Inverse of mult. by -1 is div. by -1
|
| If you put 7 back in for x in the original
problem you will see that 7 is the solution we are looking for. |
| Answer/Discussion
to 1c
|
 |
*Remove ( ) by using dist. prop.
*Combine like terms
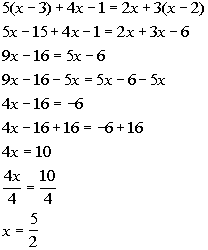
*Get all x terms
on one side
*Inverse of sub. 16 is add. 16
*Inverse of mult. by 4 is div. by 4
|
| If you put 5/2 back in for x in the original
problem you will see that 5/2 is the solution we are looking for. |
| Answer/Discussion
to 2a
|
 |
*Remove ( ) by using dist. prop.
*Combine like terms
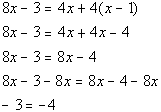
*Get all the x
terms on one side
|
| Where did our variable, x, go???
It disappeared on us. Also note how we ended up with a FALSE statement,
-3 is not equal to -4. This does not mean that x
= -3 or x = -4.
Whenever your variable drops out AND you end
up with a FALSE statement, then after all of your hard work, there is NO
SOLUTION.
So, the answer is no solution which means this is an inconsistent
equation. |
| Answer/Discussion
to 2b
|
 |
*To get rid of the fractions,
mult. both sides by the LCD of 4
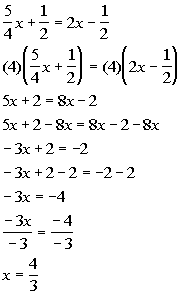
*Get all the x
terms on one side
*Inverse of add. 2 is sub. 2
*Inverse of mult. by -3 is div. by -3
|
| If you put 4/3 back in for x in the original
problem you will see that 4/3 is the solution we are looking for.
This would be an example of a conditional equation, because we came
up with one solution. |
| Answer/Discussion
to 2c
|
 |
*Remove ( ) by using dist. prop.
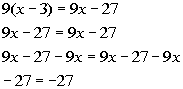
*Get all the x
terms on one side
|
| Where did our variable, x, go???
It disappeared on us. Also note how we ended up with a TRUE statement,
-27 does indeed equal -27. This does not mean that x
= -27.
Whenever your variable drops out AND you end
up with a TRUE statement, then the solution is ALL REAL NUMBERS. This
means that if you plug in any real number for x
in this equation, the left side will equal the right side.
So the answer is all real numbers, which means this equation is an
identity. |
WTAMU > Virtual Math Lab > College Algebra > Tutorial 14: Linear Equations in One Variable
All contents copyright (C) 2002 - 2008, WTAMU and Kim Seward.
All rights reserved.
Last revised on May 16, 2008 by Kim Seward.
|
