

2x - 3y = -6
Let's first find the x-intercept.
What value are we going to use for y?
You are correct if you said y = 0.
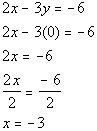
*Inverse of mult. by 2 is div. by 2
Next we will find the y- intercept.
What value are we going to plug in for x?
If you said x = 0, you are right.
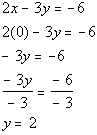
*Inverse of mult. by -3 is div. by -3
We can plug in any x value we want as long as we get the right corresponding y value and the function exists there.
Let's put in an easy number x =
1:
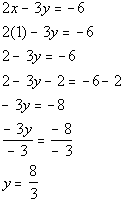
*Inverse of add 2 is sub. 2
*Inverse of mult. by -3 is div. by -3
Note that we could have plugged in any value for x: 5, 10, -25, ...,
but it is best to keep it as simple as possible.
The solutions that we found are:
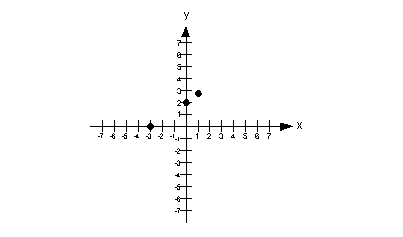
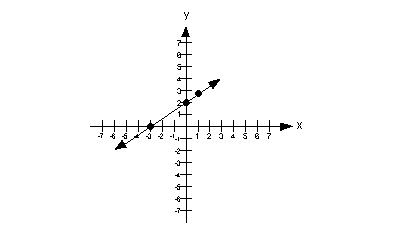
x = 3y
Let's first find the x-intercept.
What value are we going to use for y?
You are correct if you said y = 0.
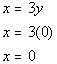
Next we will find the y- intercept.
What value are we going to plug in for x?
If you said, x = 0 you are right.
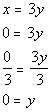
Since we really have found only one point this time, we better find two additional solutions so we have a total of three points.
We can plug in any x value we want as long as we get the right corresponding y value and the function exists there.
Let's put in an easy number x =
1:
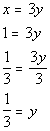
*Inverse of mult. by 3 is div. by 3
Let's put in another easy number x = -1:
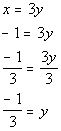
*Replace x with -1
*Inverse of mult. by 3 is div. by 3
The solutions that we found are:
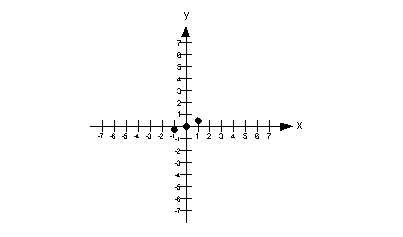
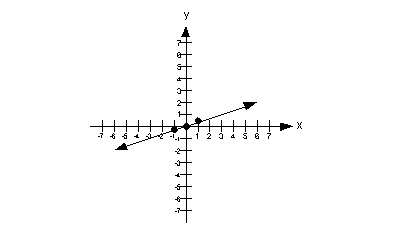
x = 4
Since this is a special type of line, I thought I would talk about steps 1 and 2 together.
It does not matter what y is, as long as x is 4.
Note that the x-intercept is at (4, 0).
Do we have a y-intercept? The answer is no. Since x can never equal 0, then there will be no y-intercept for this equation.
Some points that would be solutions are (4, 0), (4, 1), and (4, 2).
Again, I could have picked an infinite number of solutions.
The solutions that we found are:
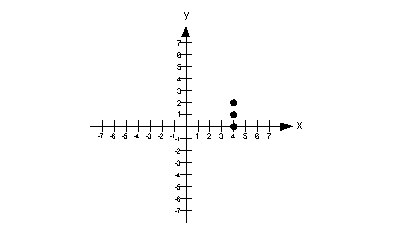
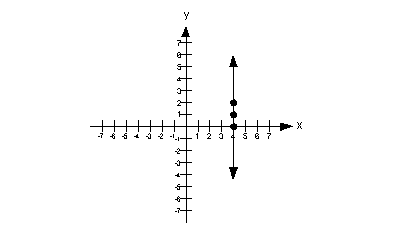
y + 5 = 0
Since this is a special type of line, I thought I would talk about steps 1 and 2 together.
It doesn't matter what x is, y is always -5. So for our solutions we just need three ordered pairs such that y = -5.
Note that the y-intercept (where x = 0) is at (0, -5).
Do we have a x-intercept? The answer is no. Since y has to be -5, then it can never equal 0, which is the criteria of an x-intercept.
So some points that we can use are (0, -5), (1, -5) and (2, -5). These are all ordered pairs that fit the criteria of y having to be -5.
Of course, we could have used other solutions, there are an infinite
number of them.
The solutions that we found are:
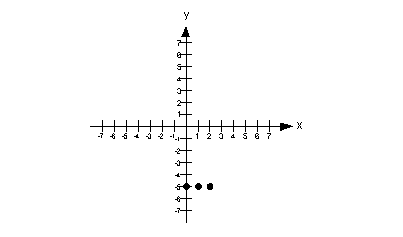
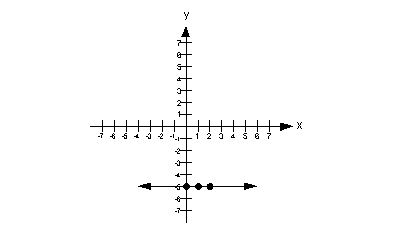
Last revised on July 31, 2011 by Kim Seward.
All contents copyright (C) 2001 - 2011, WTAMU and Kim Seward.
All rights reserved.