Intermediate Algebra
Answer/Discussion to Practice Problems
Tutorial 9: Formulas and Problem Solving
 Answer/Discussion
to 1a
I = PRT;
for T |
Do you recognize this formula?
This happens to be the formula for simple interest, where I = simple interest, P = principal, R = annual percentage rate, and T = time
in years.
In this problem we need to solve for T.
This means we need to get T on one side
and
EVERYTHING ELSE on the other side using inverse operations.
Let’s solve this formula for T: |
|
*Inverse of mult. by PR is div. by PR
*Formula solved for T
|
Answer/Discussion
to 1b
3 x - 7 y = 2; for y |
In this problem we need to solve for y.
This means we need to get y on one side
and
EVERYTHING ELSE on the other side using inverse operations.
Let’s solve this formula for y: |
|
*Inverse of add 3x is sub. 3x
*Inverse of mult. by -7 is div.
by -7
*Formula solved for y
*Divide num. by -7
*Another way to write it
|
Answer/Discussion
to 2a
A principle of $50,000 is invested into a CD paying an annual
percentage
rate of 7.5%. Find the amount in the account after 10 years if
the
account is compounded monthly. |
Make sure that you read the question carefully several
times.
Since we are looking for compound interest, we will need
the compound
interest formula:
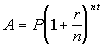
The variables in this formula represent the following:
A = end amount in the
account
P = principal (starting
amount)
r = annual rate of interest
t = time in years
n = number of times
compounded per year |
In this problem,
A = ? = this is the variable we are looking for
P = 50000
r = 7.5% = .075
t = 10
n = 12 (There are
12 months
in a year)
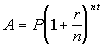
Plugging the values into the formula we get:
|
|
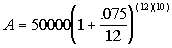
*.075/12 = .00625 and 12(10) =
120
*Add inside the ( )
*Raise 1.00625 to the exponent of
120
*Multiply |
If you take $50000 and compound it monthly for 10
years, you do end
up with 105603.23
FINAL ANSWER: The compound amount is $105603.23. |
Answer/Discussion
to 2b
In Nebraska on I-80, the speed limit is 75 mph. How long would
it take you to travel 525 miles in Nebraska on I-80 if you went
the
speed limit the whole time? |
Make sure that you read the question carefully several
times.
Since we are looking for how long it would take you to
travel, we can
use the distance/rate formula:
d = rt
The variables in this formula represent the following:
d = distance
r = rate
t = time |
In this problem,
d = 525
r = 75
t = = ? = this is the
variable we are looking
for
d = rt
Plugging the values into the formula we get:
|
|
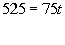
*Inverse of mult. by 75 is
div. by 75
|
If you go at a rate of 75 miles per hour for 7 hours,
you would travel
525 miles.
FINAL ANSWER: It would take 7 hours. |
Answer/Discussion
to 2c
Sally is training for the Olympics. She likes to run around
a circular track that has a diameter of 60 yards, 20 times during a
workout.
How many yards does she run during her workout? |
Make sure that you read the question carefully several
times.
Since we are needing to find the circumference of a
circle, we
can use this formula:
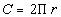
The variables in this formula represent the following:
C = circumference of a
circle
r = radius |
|
In this problem,
C = ? = this is the variable
we are looking
for
r = 30 (radius is half
of the diameter,
so r = 60/2 = 30)
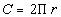
Plugging the values into the formula we get:
|
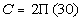
First, find the circumference of a circle. |
|
*Multiply
*Replace pi with 3.14 for an approximate
value
|
For every workout, she runs around the track 20
times. So, we
need to multiply the circumference by 20 to find the number of yards
that
she runs during her workout. |
|
*Multiply
*Multiply using approx. value
|
Last revised on July 3, 2011 by Kim Seward.
All contents copyright (C) 2001 - 2011, WTAMU and Kim Seward.
All rights reserved.
|
|
times
30 you do get 60