College Algebra
Tutorial 64: Annuities
 Learning Objectives
After completing this tutorial, you should be able to:
- Set up and solve a present value of an ordinary annuity application problem.
- Set up and solve a present value of an annuity application problem that is not ordinary.
- Set up and solve a future value of an ordinary annuity application problem.
- Set up and solve a future value of an annuity application problem that is not ordinary.
|
Introduction
In this tutorial, we will continue looking at applications of MONEY! In this tutorial, we will be learning how to find the ordinary and not ordinary future value of an annuity. We will also check out how to find the present values of those annuities. Even if you are
not
a business related major, a lot of these applications can be used with
your own finances. Annuities can be used in financing a car, IRA's, investments, etc...
It is to your benefit to step through the examples on the
page with
your calculator to make sure that you understand how to work the
problems.
Let's have some more fun working with money!!!
|
Tutorial
An annuity is a sequence of payments made at fixed periods
of time
over a given interval. |
The fixed period in an annuity is a payment period. |
The given interval in an annuity is called a term. |
|
Present Value of an Annuity
|
The present value of an annuity IS THE SUM of the present
values
of all the payments. It represents the amount that must
be invested now to purchase payments due in the future. |
In an ordinary annuity, each payment is made at the end of
a payment
period. |
In an annuity that is not ordinary, each payment is made
at the
beginning of a payment period. |
Present Value of an Ordinary Annuity
Formula
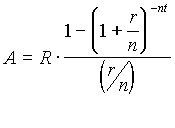
A = present value of an ordinary
annuity
R = amount per payment
r = nominal rate
n = number of periods per
year
t = number of years |
Note that some of the letters used in this formula may look
different than
the one in your book.
In some books they use P instead of A. Just note that this formula is set up to find the present value of an ordinary annuity whether you call it P or A.
Also, in some books, an i is used instead of r/n. I like to write the formula out using r/n because it helps to remind us that we need to divide the periodic rate by the number of compound periods per year.
 Example
1: Find the present value of the given (ordinary)
annuity.
$1000 per month for 15 months at a rate of 8% compounded
monthly. |
|
*12 % in decimal form
*Comp. monthly - 12 times per year
*15 months = 1.25 YEARS
*PV of an ord. annuity
*Plug in values into form.
*Calculate number inside ( )
and exponent
*Raise inside of ( ) to the
-15th power
*Calculate fraction
|
The present value of the given ordinary annuity would be
$14228.63 |
Present Value of an Annuity (Not
Ordinary)
Formula
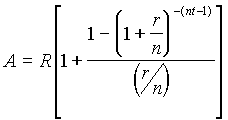
A = present value of an annuity
(not ordinary)
R = amount per payment
r = nominal rate
n = number of periods per
year
t = number of years |
Again an annuity that is not ordinary has a payment that is
due at
the beginning of a pay period, not the end. So that is why there
is a different formula - to make the proper adjustments going from
payments
made at the end of the period to payments made at the beginning of the
period.
Note that some of the letters used in this formula may look
different than
the one in your book.
In some books they use P instead of A. Just note that this formula is set up to find the present value of an ordinary annuity whether you call it P or A.
Also, in some books, an i is used instead of r/n. I like to write the formula out using r/n because it helps to remind us that we need to divide the periodic rate by the number of compound periods per year.
Example
2: Find the present value of the given annuity
due.
$1500 paid at the beginning of each six-month period for 6
years at
the rate of 9% compounded semiannually. |
|
*9 % in decimal form
*Comp. semiannually - 2 times per year
*PV of an annuity (not ord.)
*Plug in values into form.
*Calc number inside ( ) and exp.
*Raise inside of ( ) to the
-11th power
*Calculate number inside [ ]
|
The present value for the given annuity (not ordinary) is
$14293.38 |
Future Value of an Ordinary
Annuity
Formula
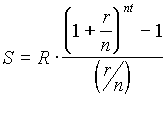
S = future value of an ordinary
annuity
R = amount per payment
r = nominal rate
n = number of periods per
year
t = number of years |
Note that some of the letters used in this formula may look
different than
the one in your book.
In some books, an i is used instead of r/n. I like to write the formula out using r/n because it helps to remind us that we need to divide the periodic rate by the number of compound periods per year.
Example
3: Find the future value of the given (ordinary)
annuity.
$1200 per month for 4 years at the rate of 15% compounded
monthly. |
|
*15 % in decimal form
*Comp. monthly - 12 times per year
*FV of an ordinary annuity
*Plug in values into form.
*Calculate number inside ( )
and exponent
*Raise inside of ( ) to the
48th power
*Calculate fraction
|
The future value of the given ordinary annuity is $78274.06 |
Future Value of an Annuity (Not
Ordinary)
Formula
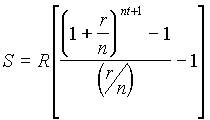
S = future value of an ordinary
annuity
R = amount per payment
r = nominal rate
n = number of periods per
year
t = number of years |
Note that some of the letters used in this formula may look
different than
the one in your book.
In some books, an i is used instead of r/n. I like to write the formula out using r/n because it helps to remind us that we need to divide the periodic rate by the number of compound periods per year.
Example
4: Find the future value of the given annuity due
(not
ordinary).
$800 each year for 15 years at the rate of 8% compounded
annually.
|
|
*8 % in decimal form
*Comp. annually - 1 time per year
*FV of an annuity (not ord.)
*Plug in values into form.
*Calc. number inside ( ) and
exp.
*Raise inside of ( ) to the
16th power
*Calculate fraction
*Calculate inside of [ ]
|
The future value of the given annuity (not ordinary) due
is $23459.43 |
Practice Problems
These are practice problems to help bring you to the next level.
It will allow you to check and see if you have an understanding of these
types of problems. Math works just like anything
else, if you want to get good at it, then you need to practice it.
Even the best athletes and musicians had help along the way and lots of
practice, practice, practice, to get good at their sport or instrument.
In fact there is no such thing as too much practice. To get the most out of these, you should work the problem out on
your own and then check your answer by clicking on the link for the answer/discussion
for that problem. At the link you will find the answer
as well as any steps that went into finding that answer. |
 Practice
Problem 1a: Find the present value of the given (ordinary) annuity.
Practice
Problem 2a: Find the present value of the given annuity.
Practice
Problem 3a: Find the future value of the given (ordinary) annuity.
Practice
Problem 4a: Find the future value of the given annuity due.
Need Extra Help on these Topics?
Last revised on October 8, 2011 by Kim Seward.
All contents copyright (C) 2002 - 2011, WTAMU and Kim Seward. All rights reserved.
|
|
