College Algebra
Tutorial 58: Probability
 Learning Objectives
After completing this tutorial, you should be able to:
- Find the probability of an empirical event.
- Find a theoretical probability.
- Know when two events are mutually exclusive.
- Use basic properties of probability to find various probabilities.
- Know when two events are independent of each other.
- Know how to find the probability of the intersection of two independent
events.
|
Introduction
In this tutorial we will be going over probability. This will include
learning some of the terminology that goes with the different aspects of
probability. Things like experiment, sample space and event to name
a few. A lot of times people associate probability with gambling,
like playing cards and lotto. It can be used to find out your chances
of winning :-) or losing :-( a game of chance. But it can also be
used in other areas like research and advertising. A doctor might
want to weigh the risks of putting a patient on a new drug and may
look at the probability of their chances of success on the drug.
A company may take a survey of people on certain products to see what is
the probability that they will pick their product. So probability
can be fun and games, but it can also be useful in a professional setting.
I think you are ready to venture into the world of probability. |
Tutorial
An experiment is an act for which the outcome is uncertain.
Examples of experiments are rolling a die, tossing a coin, surveying
a group of people on their favorite soft drink, etc... |
A sample space S for an experiment is the set of all possible
outcomes of the experiment such that each outcome corresponds to exactly
one element in S. The elements of S are called sample points.
If there is a finite number of sample points, that number is denoted n(S),
and S is said to be a finite sample space. For example, if our experiment is rolling a single die, the sample space
would be S = {1, 2, 3, 4, 5, 6}. If our experiment is tossing a single
coin, our sample space would be S = {Heads, Tails}. If our experiment
is surveying a group of people on their favorite soft drink, our sample
space would be all of the soft drinks on the survey. |
Any subset E of a sample space for an experiment
is called an event for that experiment.
For example, if our experiment is rolling a single die, an event E could be rolling an even number, thus E = {2,
4, 6}. If our experiment is tossing a single coin, an event E could be tossing a Tail, where E = {Tails}.
If our experiment is surveying a group of people on their favorite soft
drink, an event E could be picking a diet soft
drink. |
Finding the probability of an empirical event is specifically
based on direct observations or experiences.
For example, a survey may have been taken by a group of people.
If the data collected is used to find the probability of an event tied
to the survey, it would be an empirical probability.
Or if a scientist did research on a topic and recorded the outcome and
the data from this is used to find the probability of an event tied to
the research, it would also be an empirical probability. |
|
Empirical Probability Formula
|
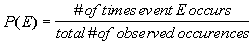
P(E) represents
the probability that an event, E, will occur.
The numerator of this probability is the number of times or ways that
specific event occurs.
The denominator of this probability is the overall number of ways that
the experiment itself could occur. |
 Example
1: The table below lists the results of a student
survey pertaining to favorite ethnic foods. Each student chose only
one type of ethnic food for the survey.
|
Type
|
Italian
|
Chinese
|
Japanese
|
Thai
|
Mexican
|
Other
|
|
Number
|
15
|
20
|
3
|
4
|
30
|
10
|
Using the given table find the probability that a) a student's favorite
ethnic food is Chinese, and b) a student's favorite ethnic food is Mexican.
Round answers to three decimal places. |
1a) a student's favorite ethnic food is Chinese: |
To find this probability, we need to know n(E)
= n(students whose favorite ethnic food is Chinese), which is the number
of students who preferred Chinese food and n(S)
= n(students surveyed), which is the total number of students surveyed.
What do you think n(E) = n(students
whose favorite ethnic food is Chinese) is?
If you said 20 you are correct. 20 students indicated that their
favorite ethnic food is Chinese.
What do you think n(S) = n(students
surveyed) is?
If you said 82 give yourself a pat on the back. If you total 15
+ 20 + 3 + 4 + 30 + 10 you get 82.
Putting this together in the Empirical Probability formula you get: |
|
*putting in the numbers found above
*reducing the fraction
*rounding to 3 decimal places |
The probability that a student's favorite
ethnic food is Chinese is .244. |
1b) a student's favorite ethnic food is Mexican: |
To find this probability, we need to know n(E)
= n(students whose favorite ethnic food is Mexican), which is the number
of students who preferred Mexican food and n(S)
= n(students surveyed), which is the total number of students surveyed.
What do you think n(E) = n(students
whose favorite ethnic food is Mexican) is?
If you said 30 you are correct. 30 students indicated that their
favorite ethnic food is Mexican.
What do you think n(S) = n(students
surveyed) is?
If you said 82 give yourself a pat on the back. As found in example
1a above, the total surveyed is 82.
Putting this together in the Empirical Probability formula you get: |
|
*putting in the numbers found above
*reducing the fraction
*rounding to 3 decimal places |
The probability that a student's favorite
ethnic food is Mexican is .366. |
A sample space S is called an equiprobable
space if and only if all the simple events are equally likely to
occur.
Some quick examples of this are:
| A toss of a fair coin. It is equally likely for a head
to show up as it is for a tail.
Select a name at random from a hat. Since it is at random,
each name is equally likely to be picked.
Throwing a well balanced die. Each number on the die has
the same amount of chance of coming up. |
|
Theoretical probability is finding the probability of events
that come from an equiprobable sample space or, in other words, a sample space of known equally likely outcomes.
For example, finding various probabilities dealing with the roll of
a die, a toss of a coin, or a picking of a name from a hat. |
|
Theoretical Probability Formula
|
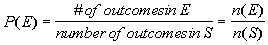
If E is an event of sample space S,
where n(E) is the number of equally likely
outcomes of event E and n(S)
is the number of equally outcomes of sample space S,
then the probability of event E occurring can
be found using the Theoretical Probability Formula above. |
In general, events E and F are said to be mutually exclusive if and only if they have
no elements in common.
For example, if the sample space is rolling a die, where S = {1, 2, 3, 4, 5, 6}, and E is the event of
rolling an even number, E = {2, 4, 6} and F is the event of rolling an odd number, F = {1, 3, 5}, E and F are mutually exclusive, because they
have NO elements in common. Now lets say that event G is rolling a number less than 4, G = {1, 2, 3}. Would event G and E be mutually exclusive? If you said
no, you are correct, they have one element, the number 2, in common. G and F would not be mutually exclusive either. |
|
Properties of Probability
|
|
Property 1
|
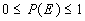
It stands to reason that if the bottom number of the probability is
the total number - which is the highest number - than the probability
will never exceed 1. |
|
Property 2
|
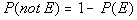
Either an element is in E or it is not
in E.
So if, P(E) = 1/4 then P(not E)
= 3/4. |
|
Property 3
|
|
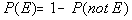
Property 4
"Or" probabilities with
mutually exclusive events
|
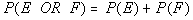
Since we are dealing with sets that are mutually
exclusive, this means they have no elements in common. So
we can just add the two probabilities together without running a risk of
having something counted twice. |
|
Property 5
"Or" probabilities with events that are NOT mutually
exclusive
|
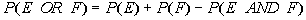
Since we are dealing with events that are NOT mutually exclusive, we
run the risk of elements being counted twice if we just add them together
as in Property 4 above.
You need to subtract the intersection to get rid of the elements that
were counted twice. In other words, you may have some
elements in common, so if we add the number of elements in E to the number of elements of F, we may
be adding some elements twice, so to avoid this we need to subtract the
number of elements in the intersection of the two events - which would
be all the elements that are in both sets. |
Example
2: A pair of fair dice is tossed. Determine
the probability that a) at least one of the dice shows a 6 and b) the sum
of the two numbers is 5. Round answers to three decimal places.
Here is a table of all the possible outcomes of having a pair of dice
tossed:
|
(1, 1)
|
(1, 2)
|
(1, 3)
|
(1, 4)
|
(1, 5)
|
(1, 6)
|
|
(2, 1)
|
(2, 2)
|
(2, 3)
|
(2, 4)
|
(2, 5)
|
(2, 6)
|
|
(3, 1)
|
(3, 2)
|
(3, 3)
|
(3, 4)
|
(3, 5)
|
(3, 6)
|
|
(4, 1)
|
(4, 2)
|
(4, 3)
|
(4, 4)
|
(4, 5)
|
(4, 6)
|
|
(5, 1)
|
(5, 2)
|
(5, 3)
|
(5, 4)
|
(5, 5)
|
(5, 6)
|
|
(6, 1)
|
(6, 2)
|
(6, 3)
|
(6, 4)
|
(6, 5)
|
(6, 6)
|
|
2a) at least one of the dice shows a 6: |
To find this probability we need to know n(E)
= n(at least one of the dice shows a 6), which is the number of rolls of
two dice that have at least one 6 showing and n(S)
= n(rolls of a pair of fair dice), which is the total number of ways a
pair of fair dice can be rolled.
What do you think n(E)
= n(at least one of the dice shows a 6) is?
If you said 11 you are correct. Looking at the table
above, there are 11 rolls of two dice that contain at least one
6.
What do you think n(S)
= n(rolls of a pair of fair dice) is?
If you said 36 give yourself a pat on the back. Looking at the table
above, there are 36 possible rolls of two fair dice.
Putting this together in the Theoretical Probability formula you
get: |
|
*putting in the numbers found above
*rounding to 3 decimal places |
The probability that at least one of the dice shows a 6 is .306. |
2b) the sum of the two numbers is 5: |
To find this probability we need to know n(E)
= n(the sum of the two numbers is 5), which is the number of rolls of two
dice that have a sum of 5 and n(S)
= n(rolls of a pair of fair dice), which is the total number of ways a
pair of fair dice can be rolled.
What do you think n(E)
= n(the sum of the two numbers is 5) is?
If you said 4 you are correct. Looking at the table
above, 4 rolls of two die {(4, 1), (3, 2), (2, 3), (1, 4)} have
a sum of 5.
What do you think n(S)
= n(rolls of a pair of fair dice) is?
If you said 36 give yourself a pat on the back. Looking at the table
above, there are 36 possible rolls of two fair dice.
Putting this together in the Theoretical Probability formula you
get: |
|
*putting in the numbers found above
*reducing the fraction
*rounding to 3 decimal places |
The probability that the sum of the two numbers is 5 is .111. |
Example
3: From a group of 10 women and 5 men, 2 people
are selected at random to form a committee. Find the probability
that a) only men are selected and b) exactly 1 man and 1 woman is selected.
Round answers to three decimal places. |
3a) only men are selected: |
To find this probability we need to know n(E)
= n(only men are selected), which is the number of committees that contain
2 men and n(S) = n(2 person committees), which
is the total number of 2 person committees.
What do you think n(E)
= n(only men are selected) is?
Since we are counting committees that means we are counting groups of
people, which means we need to use combinations to count them. If
you need a review on combinations, feel free to go to Tutorial
57: Combinations.
If you said 10 you are correct.
Let's see how we get that number.
Here is what the committee looks like: we would have to have
2 men to meet this condition:
2 MEN
|
|
*Comb. of n = 5 men taken r = 2 at a time
*Eval. inside ( )
*Expand 5! until it gets to 3!
which is the larger ! in the den.
*Cancel out 3!'s
|
As mentioned above, n(E) = n(only men are
selected) = 10.
If you have a factorial key, you can put it in as 5!, divided by
3!, divided by 2! and then press enter or =.
If you don't have a factorial key, you can simplify it as shown above
and then enter it in. |
What do you think n(S)
= n(2 person committees) is?
If you said 105 give yourself a pat on the back.
Again you would have to use combinations to figure this one out.
Overall, there are 10 women and 5 men for a total of 15 people, taken 2
at a time. |
 |
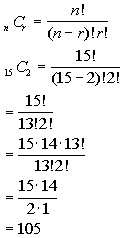*Comb. of n = 15 people taken r = 2 at a time
*Eval. inside ( )
*Expand 15! until it gets to 13!
which is the larger ! in the den.
*Cancel out 13!'s
|
As mentioned above, n(S) = n(2 person committees) = 105.
If you have a factorial key, you can put it in as 15!, divided by
13!, divided by 2! and then press enter or =.
If you don't have a factorial key, you can simplify it as shown above
and then enter it in.
Putting this together in the Theoretical Probability formula you
get: |
|
*putting in the numbers found above
*reducing the fraction
*rounding to 3 decimal places |
The probability that only men are selected is .095. |
3b) exactly 1 man and 1 woman: |
To find this probability we need to know n(E)
= n(1 man and 1 woman are selected), which is the number of committees
that contain 1 man and 1 woman and n(S) = n(2
person committees), which is the total number of 2 person committees.
What do you think n(E)
= n(1 man and 1 woman are selected) is?
Since we are counting committees that means we are counting groups of
people, which means we need to use combinations to count them. If
you need a review on combinations, feel free to go to Tutorial
57: Combinations.
If you said 50 you are correct.
Let's see how we get that number.
Here is what the committee looks like: we would have to have
1 man and 1 woman to meet this condition:
1 MAN 1 WOMAN
|
|
*Comb. of n = 5 men taken r = 1 at a time
*Comb. of n = 10 women taken r = 1 at a time
*Eval. inside ( )
*Expand 5! until it gets to 4! and 10! until
it gets to 9!
which are the larger !'s in the den.
*Cancel out 4!'s and 9!'s
|
As mentioned above, n(E) = n(1 man and
1 woman selected) = 50.
If you have a factorial key, you can put it in as 5!, divided by
4!, divided by 1! times 10!, divided by 9!, divided by 1! and then press
enter or =.
If you don't have a factorial key, you can simplify it as shown above
and then enter it in. |
What do you think n(S)
= n(2 person committees) is?
If you said 105 give yourself a pat on the back. As found in example
3a above, the total number of 2 person committees is 105. |
| Putting this together in the Theoretical Probability formula you
get: |
|
*putting in the numbers found above
*reducing the fraction
*rounding to 3 decimal places |
The probability that exactly one man and one woman are selected is
.476. |
Example
4: One student's name will be picked at random to
win a CD player. There are 12 male seniors, 15 female seniors, 10
male juniors, 5 female juniors, 2 male sophomores, 4 female sophomores,
11 male freshmen and 12 female freshman. Find the probability that
a) a senior or a junior is picked, b) a freshman or a female is picked,
and c) a freshman is NOT picked. Round answers to three decimal
places. |
4a) a senior or a junior is picked: |
|
Let's break it down first by finding each separate probability.
P(a senior is picked)
To find this probability we need to know n(E)
= n(seniors), which is the number of seniors and n(S)
= n(students), which is the total number of students.
What do you think n(E)
= n(seniors) is?
If you said 27 you are correct. There are 12 male seniors and
15 female seniors for a total of 27 seniors.
What do you think n(S)
= n(students) is?
If you said 71 give yourself a pat on the back. If we add all
the students together we get 71.
Putting this together in the Theoretical Probability formula you
get: |
|
*putting in the numbers found above
*rounding to 3 decimal places |
|
P(a junior is picked)
To find this probability we need to know n(E)
= n(juniors), which is the number of juniors and n(S)
= n(students), which is the total number of students.
What do you think n(E)
= n(juniors) is?
If you said 15 you are correct. There are 10 male juniors and
5 female juniors for a total of 15 juniors.
What do you think n(S)
= n(students) is?
If you said 71 give yourself a pat on the back. If we add all
the students together we get 71.
Putting this together in the Theoretical Probability formula you
get: |
|
*putting in the numbers found above
*rounding to 3 decimal places |
Putting the two probabilities of mutually exclusive events together
we get: |
|
*putting in the numbers found above
*rounding to 3 decimal places |
The probability that a senior or a junior is picked is .592. |
4b) a freshman or a female is picked: |
Note that these two events are NOT mutually exclusive. You CAN
be a freshman and a female at the same time. So we can use the formula
(property 5):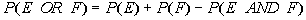
Let's break it down first by finding each separate probability.
P(a freshman is picked)
To find this probability we need to know n(E)
= n(freshmen), which is the number of freshmen and n(S)
= n(students), which is the total number of students.
What do you think n(E)
= n(freshmen) is?
If you said 23 you are correct. There are 11 male freshmen and
12 female freshmen for a total of 23 freshmen.
What do you think n(S)
= n(students) is?
If you said 71 give yourself a pat on the back. If we add all
the students together we get 71.
Putting this together in the Theoretical Probability formula you
get: |
|
*putting in the numbers found above
*rounding to 3 decimal places |
|
P(a female is picked)
To find this probability we need to know n(E)
= n(females), which is the number of females and n(S)
= n(students), which is the total number of students.
What do you think n(E)
= n(females) is?
If you said 36 you are correct. There are 15 female seniors, 5
female juniors, 4 female sophomores and 12 female freshman for a total
of 36 females.
What do you think n(S)
= n(students) is?
If you said 71 give yourself a pat on the back. If we add all
the students together we get 71.
Putting this together in the Theoretical Probability formula you
get: |
|
*putting in the numbers found above
*rounding to 3 decimal places |
|
P(a freshman AND female is picked)
To find this probability we need to know n(E)
= n(freshman AND female), which is the number of female freshmen and n(S)
= n(students), which is the total number of students.
What do you think n(E)
= n(freshmen AND female) is?
If you said 12 you are correct. There are 12 female freshmen.
What do you think n(S)
= n(students) is?
If you said 71 give yourself a pat on the back. If we add all
the students together we get 71.
Putting this together in the Theoretical Probability formula you
get: |
|
*putting in the numbers found above
*rounding to 3 decimal places |
Putting the probabilities of non mutually exclusive events together
we get: |
|
*putting in the numbers found above
*rounding to 3 decimal places |
The probability that a freshman or a female is picked is .662. |
4c) a freshman is NOT picked: |
One way we can approach this is to use Property
2: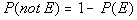
To find this probability we need to know n(E)
= n(freshmen), which is the number of freshman and n(S)
= n(students), which is the total number of students.
What do you think n(E)
= n(freshmen) is?
If you said 23 you are correct. There are 11 male freshmen and
12 female freshmen for a total of 23 freshman.
What do you think n(S)
= n(students) is?
If you said 71 give yourself a pat on the back. If we add all
the students together we get 71.
Putting this together in the Theoretical Probability formula you
get: |
|
*putting in the numbers found above
*rounding to 3 decimal places |
|
So, the probability a student picked is NOT a freshman is |
|
*putting in the numbers found above
*rounding to 3 decimal places
|
The probability that a freshman is NOT picked is .676. |
|
Independent Events
E and F are Independent Events if an
only if
|
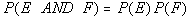
| Two events are independent of each other if the outcome of one event
does not affect the outcome of the other event.
You can use this formula to show if two events are independent or not. |
Example
5: If two cards are drawn from a deck of cards,
WITH REPLACEMENT, find the probability that the 1st card is a heart AND
the 2nd card is an ace. Round answer to three decimal places. |
Since it said WITH REPLACEMENT, that means the outcome of the 1st card
does NOT affect the outcome of the 2nd card, which means these
two events are independent. So we can use the formula 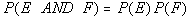to find our probability.
Let's break it down. |
P(1st card is a heart)
To find this probability we need to know n(E)
= n(hearts), which is the number of hearts in a deck of cards and n(S)
= n(cards), which is the total number of cards in a deck.
What do you think n(E)
= n(hearts) is?
If you said 13 you are correct. There are 13 cards in a deck that have
heart on them.
What do you think n(S)
= n(cards) is?
If you said 52 give yourself a pat on the back. There are 52 cards in
a deck.
Putting this together in the Theoretical Probability formula you
get: |
|
*putting in the numbers found above
*reducing the fraction
*rounding to 3 decimal places
|
|
P(2nd card is an ace)
To find this probability we need to know n(E)
= n(aces), which is the number of aces in a deck of cards and n(S)
= n(cards), which is the total number of cards in a deck.
What do you think n(E)
= n(aces) is?
If you said 4 you are correct. There are 4 cards in a deck that have
an ace on them.
What do you think n(S)
= n(cards) is?
If you said 52 give yourself a pat on the back. There are 52 cards in
a
deck.
Putting this together in the Theoretical Probability formula you
get: |
|
*putting in the numbers found above
*reducing the fraction
*rounding to 3 decimal places
|
Putting the probabilities of two events that are independent together
we get: |
|
*putting in the numbers found above
*rounding to 3 decimal places
|
Practice Problems
These are practice problems to help bring you to the next level.
It will allow you to check and see if you have an understanding of these
types of problems. Math works just like anything
else, if you want to get good at it, then you need to practice it.
Even the best athletes and musicians had help along the way and lots of
practice, practice, practice, to get good at their sport or instrument.
In fact there is no such thing as too much practice.
To get the most out of these, you should work the problem out on
your own and then check your answer by clicking on the link for the answer/discussion
for that problem. At the link you will find the answer
as well as any steps that went into finding that answer. |
 Practice Problems 1a - 1b:
The table below lists the results of a student survey
pertaining to favorite types of music.
|
Music
|
Rock
|
Jazz
|
Country
|
Classical
|
Rap
|
|
Number
|
51
|
24
|
33
|
5
|
15
|
Using the given table find the probability that
Practice Problems 2a - 2e: You are dealt one card. Find the probability
that you are dealt
Practice Problems 3a - 3b: From a group of 7 freshmen, 9 sophomores, 8 juniors,
and 10 seniors, 6 names will be drawn. Find the probability that
Practice Problems 4a - 4b: You roll a single die two times. Find the probability
that
4a. a six is rolled the 1st time and an odd number is rolled a 2nd
time. Round answer to three decimal places.
(answer/discussion
to 4a) |
4b. a number less than or equal to 2 is rolled the 1st time and an
even number is rolled the 2nd time. Round answer to three decimal
places.
(answer/discussion
to 4b) |
Need Extra Help on these Topics?
Last revised on May 21, 2011 by Kim Seward.
All contents copyright (C) 2002 - 2011, WTAMU and Kim Seward. All rights reserved.
|
|
