Answer:

I'm going to chose to use the elimination by addition method, however it would be perfectly fine for you to use the substitution method.  Either way the answer will be the same.

Multiplying each equation by it's respective LCD we get:

Multiplying the first equation by -2 and then adding the resulting equations together we get:

Solving for x we get:

Plugging in -6 for x into the first simplified equation to find y's value, we get:

(-6, 3) is the solution to this system.

Answer:

I'm going to chose to use the substitution method, however it would be perfectly fine for you to use the elimination by addition method.  Either way the answer will be the same.

Second equation solved for x:

Substituting the expression 3y + 5 for x into the first equation and solving for y we get:

Since the variable dropped out AND we have a TRUE statement, then when have an infinite number of solutions.  They end up being the same line.

Two ways to write the answer are {(x, y)| 2x - 6y = 10} OR {(x, y) | x = 3y + 5}.

Answer:

I'm going to chose to use the elimination by addition method, however it would be perfectly fine for you to use the substitution method.  Either way the answer will be the same.

Eliminating z from equations (1) and (2) we get:

Eliminating z from equations (1) and (3) we get:

Putting equations (4) and (5) together into a system of two equations and two unknowns we get:

Eliminating y from equations (4) and (5) we get:

Solving for x we get:

Plugging 2 in for x in equation (4) and solving for y we get:

Plugging in 2 for x and -1 for y in equation (1) and solving for z we get:

(2, -1, 3) is the solution to our system.

Answer:

Let x = the rate of the boat in still water

Let y = the rate of the current.
 
 

Using the fact that (Rate)(Time) = Distance, we get the system:

Simplifying this system we get:

Eliminating the x's we get:

Solving for y we get:

Plugging 5 in for y in the first simplified equation and solving for x we get:

The speed of the boat in still water is 25 mph and the rate of the current is 5 mph.

Answer:

Let n = the number of nickels
Let d = the number of dimes
Let q = the number of quarters

The value of the coins is $5.50:

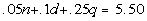
The number of nickels is three times that of the dimes:

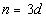
The number of nickels is six more than twice the number of quarters:

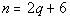
Putting this together in a system we get:

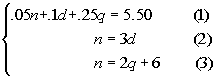
Simplifying the system we get:

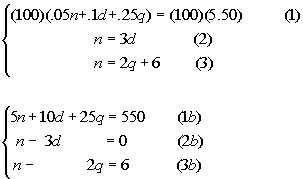
Eliminating n from equations (1b) and (2b) we get:

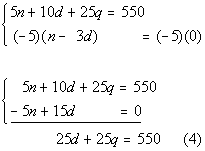
Eliminating n from equations (2b) and (3b) we get:

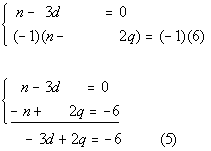
Putting equations (4) and (5) together into a system of two equations and two unknowns we get:

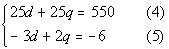
Eliminating d from equations (4) and (5) we get:

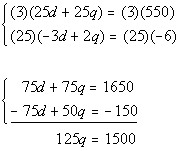
Solving for q we get:

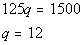
Plugging in 12 for q in equation (3) and solving for n we get:

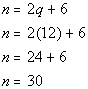
Plugging in 30 for n in equation (2) we get:

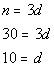
There are 30 nickels, 10 dimes and 12 quarters.

Answer:

I'm going to chose to use the elimination by addition method.  Note that this one would be very difficult to try to solve it by the substitution method.

Eliminating the x squared terms we get:

Solving for y we get:

Plugging 2 in for y in the first equation and solving for x we get:

Two solutions are (3, 2) and (-3, 2).
 

Plugging -2 in for y in the first equation and solving for x we get:

Two more solutions are (3, -2) and (-3, -2).
 

The four solutions are (3, 2), (-3, 2), (3, -2), and (-3, -2).

Answer:

I'm going to chose to use the substitution method, however it would be perfectly find for you to use the elimination by addition method.  Either way the answer will be the same.

Second equation solved for y:

Substituting the expression x for y into the first equation and solving for x: 

This will not factor so we will need to use the quadratic formula to solve:

Since, we have a negative in the square root, this means we did not get real number answer for x.

The answer is no solution.