College Algebra
Tutorial 42: Exponential Functions
 Learning Objectives Learning Objectives
After completing this tutorial, you should be able to:
- Use the exponent and e keys on your
calculator.
- Evaluate an exponential function.
- Graph exponential functions.
- Calculate compound interest problems.
|
 Introduction Introduction
In this tutorial we will be looking at exponential
functions.
It is good to be familiar with exponents in general before you start
this
lesson. What is different in this tutorial is that your variable x is now your exponent, where before, the variable x was in your base. I can’t stress this enough, if you
are not comfortable with the basics of exponents you need to
review
exponents which you can find in Tutorial
2: Integer Exponents. One thing we will be looking at in
this section is using your exponent and e keys on your
calculator.
So make sure that you have your calculator ready to go. It will
also
help you with the graphing problems. Let's say we take a look at
these exponential functions. |
 Tutorial Tutorial
Definition of
Exponential Function
The function f defined by
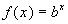
where b > 0, b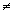 1,
and the exponent x is any real number, is called an exponential
function. 1,
and the exponent x is any real number, is called an exponential
function.
|
Again, note that the variable x is
in the
exponent as opposed to the base when we are dealing with an exponential
functions.
Also note that in this definition, the base b is restricted to being a positive number other than 1. |
Exponent Key
on Calculator
|
Before we get going with the actual exponential
functions, I wanted
to make sure that everyone knew how to use the exponent key on their
calculator.
Since there are a lot of different calculators I will be go over the
more
common ones. At this point you need to check to make sure that
you
know how to use your exponent key, because we will be using it heavily
throughout this as well as the next unit.
The two main exponent keys
found on calculators
are (you will only have one of these):
Caret top key:
^
|
Base raised to an
exponent key:
 OR
OR 
|
Check to see if you have one of the two main type of
exponent keys
(you won’t have both). If you don’t have one check the
other.
If you don’t see either, look in the reference manual that came with
the
calculator to see which key it is.
The caret top key is
most frequently found
on graphing calculators but can be found on other types of calculators.
On most graphing calculators your exponent key is the caret top
key:
^.
If you have the caret top key let's practice
taking 15 and raising
it to the 5th power. To do this you would type in 15^5 and press
your enter or = key. If you got 759375,
you
entered it in correctly. If not, try again. If you still
can't
get it look in your reference manual that came with the
calculator.
The key that look
like 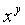 OR
OR 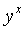 are
most
common in business and scientific calculators, but can be found on
other
types of calculators. are
most
common in business and scientific calculators, but can be found on
other
types of calculators.
On most business and scientific calculators, the exponent key looks
like 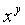 or
or 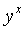 or very similar to this . or very similar to this .
If you have this key let's practice taking 15 and
raising it to
the 5th power. In this situation, you first type in your base
then
you activate your exponent key and then you type in your exponent and
then
press enter or equal. Go ahead and try it out by finding 15
raised
to the 5th power. Type in 15, then press 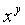 or
or 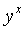 and then
type in
5 and press the enter or equal key. You should have gotten 759375
as your answer. If not, try again. If you still can't
get
it look in your reference manual that came with the calculator. and then
type in
5 and press the enter or equal key. You should have gotten 759375
as your answer. If not, try again. If you still can't
get
it look in your reference manual that came with the calculator. |
|
|
Base e
e is approximately
2.718281828...
|
The exponential function with base e is
called the natural exponential function.
e has a value attached it
(similar to pi). e is approximately
2.718281828...
This base is used in economic analysis and problems
involving natural
growth and decay.
At this point, we are just going to learn how to find
the value of e raised to an exponent using the calculator. |
I want to make sure that everyone knows how to use the e key on their calculator. Since there are a lot of different
calculators
I will be go over the more common ones. At this point you need to
check to make sure that you know how to use this key, because we will
be
using it heavily.
The two main e keys found on calculators are (you will only have one of these):
e key and
the Caret top key:
(2 keys)
e and then ^
|
e raised to
an exponent key:
(1 key)
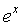
|
Check to see if you have one of the two main type of e keys (you won’t have both). If you don’t have one check the
other. If you don’t see either, look in the reference manual that
came with the calculator to see which key it is.
Having to use the e key with the caret top key is most frequently found on graphing
calculators
but can be found on other types of calculators.
On most graphing calculators in order to raise e to a power you must press the e key
first,
then press your exponent key ^, and then enter in your
exponent.
If you have the e key (with no exponent
showing)
and the caret top key let's practice taking e and
raising it to the 5th power. To do this you would press the e key, then press the exponent key ^, and then type in 5. It
should look like this on your screen: e^5. If you got
148.41316..., you entered it in correctly. If not, try again. If
you still can't get it look in your reference manual that came with the
calculator.
The key that looks
like 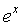 is most common in business and scientific calculators, but can be found
on other types of calculators. is most common in business and scientific calculators, but can be found
on other types of calculators.
On most business and scientific calculators, the e function key looks like 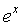 or very similar to this. So check for this key - note that
the difference between this and the one above is that this key has a
variable
exponent showing on the key - the above key only has an e (no
exponent. If you have this key let's practice taking e and raising it to the 5th power. In this situation, you
first
type in your exponent and then you activate your or very similar to this. So check for this key - note that
the difference between this and the one above is that this key has a
variable
exponent showing on the key - the above key only has an e (no
exponent. If you have this key let's practice taking e and raising it to the 5th power. In this situation, you
first
type in your exponent and then you activate your 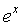 key. Go ahead and try it out by finding e raised to the 5th power. Type in 5 and then press key. Go ahead and try it out by finding e raised to the 5th power. Type in 5 and then press 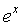 .
You should have gotten 148.41316... as your answer. If not, try
again. If
you still can't get it look in your reference manual that came with the
calculator. .
You should have gotten 148.41316... as your answer. If not, try
again. If
you still can't get it look in your reference manual that came with the
calculator. |
|
Using the Calculator,
in general
|
As mentioned above there are a lot of different types
of calculators
out there. I want to mention a few things about putting in
formulas.
Graphing calculators:
Most graphing calculators allow you to put in the whole formula before
you press enter. In fact you are able to see it all. If you
are going to plug in the whole formula at one time, just make sure you
are careful. Pay special attention to putting in the parenthesis
in the right place.
Business and scientific calculators:
On most business and scientific calculators you will have to put the
formula in part by part. Work your way inside out of the
parenthesis. DO
NOT round until you are at the end. As you go step by step,
don't
erase what you have on your calculator screen, but use it in the next
step,
so you will have have the full decimal number. The examples are
set
up to show you how to piece it together - it goes step by step.
All calculators:
DO NOT round until you get to the final answer.
You will
note on a lot of the examples that I put dots after my numbers that
would
keep going on an on if I had more space on my calculator. Keep in
mind that your calculator may have fewer or more spaces than my
calculator
does - so your calculator may have a slightly different answer
than
mine due to rounding. It should be very close though.
Make sure that you go through
these examples
with your calculator to check to make sure you are
entering in everything ok.
If you are
having problems check your reference book that came with your
calculator
or ask your math teacher about it. |
 Example
1 Example
1: Approximate the number 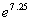 using
a calculator. Round to four decimal places. |
Try this using your calculator and see if you get the
answer that I
got. If you didn’t, refer back to e key on calculator that I have above. |
 Example
2 Example
2: Approximate the number 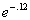 using
a calculator. Round to four decimal places. |
Try this using your calculator and see if you get the
answer that I
got. If you didn’t, refer back to e key on calculator that I have above. |
Graphing
Exponential Functions
|
Step 1: Find ordered
pairs. |
I have found that the best way to do this is to do it
the same each
time. In other words, put in the same values for x each time and then find it’s corresponding y value for the given function. |
This done exactly the same way you plotted points when
you graphed
lines and parabolas. |
The basic curve of an exponential function looks
like the following: |
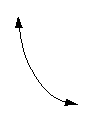
|
OR
|
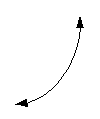
|
 Example
3 Example
3: Graph the function 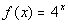 . |
Note that the base = 4 and the exponent is our variable x.
Also note, that it is in the basic form given by the definition
above,
in other words there are no other factors effecting this function. |
 Example
4 Example
4: Graph the function 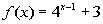 . |
Note that the base = 4 and the exponent is x - 1. There are two outside factors, we are subtracting 1 from our
variable x in the exponent AND we are adding 3 to our base after we raise it to
the
exponent x - 1. |
 Example
5 Example
5: Graph the function 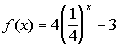 . |
Note that the base = 1/4 and the exponent is our
variable x.
This time there are two outside factors, we are multiplying our
basic
form by 4 and then we are subtracting 3.
Be careful that you use the order of operations when
working a problem
like this. We need to deal with the exponent first BEFORE we
multiply
by 4. It is really tempting to cross the 4 on the outside with
the
4 in the denominator of our base. But the 4 in the denominator is
enclosed by a ( ) with an exponent attached to it, so we have to deal
with
that first before getting the 4 on the outside involved.
Let’s find some order pairs. Again, we will use the same
input values
for x we used in examples 3 and 4 and
find
the corresponding output values for this exponential function. |
|
Compound Amount and Interest
|
Compound interest means that at the end of each
interest period the
interest earned for that period is added to the previous principle (the
invested amount) so that, it too, earns interest over the next interest
period. In other words this is an accumulative interest. |
Compound Interest
Formula
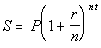
where,
S = compound or
accumulated amount
P = Principal
(starting
value)
r = nominal rate (annual
% rate)
n = the number of compound
periods per
year
t = number of years |
Note that this formula may
look different
than the one from your math book. Sometimes an A is used
for
compound or accumulated interest instead of an S.
Also sometimes r represents a periodic rate where
in
the above formula it is a nominal rate. In that type of
formula
you would not see r being divided by n,
but you would still need to do that if your r represents a periodic rate. It just isn't shown as part of the
formula.
Just keep in mind that no matter how the formula
looks the concept
is the same. |
 Example
6 Example
6: Find the a) compound amount AND b) the
compound
interest for the given investment and rate.
$15000 for 14 years at an annual rate of 5% compounded
monthly. |
Note that the steps shown in
examples 6, 7,
and 8 go with how to put it piece by piece into a business or
scientific
calculator. If you have a graphing calculator, you can chose to
do
it this way (piece by piece) or you can plug the whole formula in and
then
press enter to get your final answer.
Also note that different
calculators round
to different place values. So when you are putting this
into
your calculator keep in mind that yours may be rounding to a different
place than mine, so it may be slightly different for the last digit to
the right of the decimal. Also, don’t round anything until
you get to the final answer. For example if you round to 2
decimal
places in the first step, then your final answer may be off. You
want to keep as close to the numbers as possible, so go with whatever
your
calculator gives you and then round when you write your final answer. |
P = 15000
r = 5% = .05
t = 14
n = monthly = 12 times a year |
|
*Plug in values shown above
into compound form.
*Find number inside the (
) first
*Raise the ( ) to
the 168th power
*Multiply |
So the compound AMOUNT would be $30162.39
The compound amount is the total amount that is in the
account. How
do you think we are going to get the interest?? Well we have the
principle
which is the beginning amount and we have the compound amount which is
the end result. Looks like, if we take the difference of the two, that
will give us how much interest was earned from beginning to end. What
do
you think?
Compound amount - principle: 30162.39 - 15000 =
15162.39
So our compound interest is $15162.39.
Wow, our money doubled and then some - of course it
compounded 168 times. |
 Example
7 Example
7: Find the a) compound amount AND b) the
compound
interest for the given investment and rate.
$20500 for 15 years at an annual rate of 7.5% compounded
semiannually. |
P = 20500
r = 7.5% = .075
t = 15
n = semiannually = 2 times a
year. |
|
*Plug in values shown above
into compound form.
*Find number inside the (
) first
*Raise the ( ) to
the 30th power
*Multiply |
So the compound AMOUNT would be $61858.16
The compound amount is the total amount that is in the
account. How
do you think we are going to get the interest?? Well we have the
principle
which is the beginning amount and we have the compound amount which is
the end result. Looks like, if we take the difference of the two, that
will give us how much interest was earned from beginning to end. What
do
you think?
Compound amount - principle: 61858.16 - 20500 =
41358.16
So our compound interest is $41358.16. |
Compound Continuously
Formula
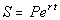
where,
S = compound or
accumulated amount
P = Principal
(starting
value)
r = nominal rate (annual
% rate)
t = number of years |
Compounded continuously means that it is compounded at
every instant
of time.
Note that this formula may look
different than
the one from your math book. Sometimes an A is used for
compound
or accumulated interest instead of an S.
Just keep in mind that no matter how the formula
looks the concept
is the same. |
 Example
8 Example
8: Find the accumulated value of an investment
of
$5000 that is compounded continuously for four years at an interest
rate
of 4.5%. |
P = 5000
r = 4.5% = .045
t = 4 |
|
*Plug in values shown above into
compound
form.
*Raise e to the
18th power
*Multiply
|
So the accumulated or compound AMOUNT would be
$5986.09 |
 Practice Problems Practice Problems
These are practice problems to help bring you to the next level.
It will allow you to check and see if you have an understanding of these
types of problems. Math works just like anything
else, if you want to get good at it, then you need to practice it.
Even the best athletes and musicians had help along the way and lots of
practice, practice, practice, to get good at their sport or instrument.
In fact there is no such thing as too much practice.
To get the most out of these, you should work the problem out on
your own and then check your answer by clicking on the link for the answer/discussion
for that problem. At the link you will find the answer
as well as any steps that went into finding that answer. |
 Practice Problems 1a - 1b: Approximate the given number
using a calculator.
Round to four decimal places. Practice Problems 1a - 1b: Approximate the given number
using a calculator.
Round to four decimal places.
 Practice Problems 2a - 2b: Graph the given function. Practice Problems 2a - 2b: Graph the given function.
 Practice Problems 3a - 3b: Find the a) compound amount AND
b) the compound
interest for the given investment and rate. Practice Problems 3a - 3b: Find the a) compound amount AND
b) the compound
interest for the given investment and rate.
 Practice Problem 4a: Find the accumulated value for
the given investment
and rate. Practice Problem 4a: Find the accumulated value for
the given investment
and rate.
 Need Extra Help on these Topics? Need Extra Help on these Topics?

Last revised on March 21, 2011 by Kim Seward.
All contents copyright (C) 2002 - 2011, WTAMU and Kim Seward. All rights reserved.
|
|


