College Algebra
Answer/Discussion to Practice Problems
Tutorial 32: Graphs of Functions, Part II:
Domain/Range, Vertical Line Test, Increasing/Decreasing/Constant Functions, Even/Odd Functions, and Greatest Integer Function
 Answer/Discussion
to 1a Answer/Discussion
to 1a
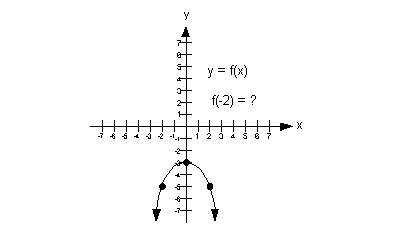
|
a) Domain
We need to find the set of all input values. In terms of ordered
pairs, that correlates with the first component of each one. In
terms
of this two dimensional graph, that corresponds with the x values
(horizontal axis).
Since that is the case, we need to look to the left and
right and see
if there are any end points. In
this case, note how there are arrows on both ends of the graph and
no end points. This means that the graph goes on and on forever
in
both directions.
This means that the domain is 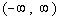 . . |
b) Range
We need to find the set of all output values. In terms of ordered
pairs, that correlates with the second component of each one. In terms
of this two dimensional graph, that corresponds with the y values (vertical axis).
Since that is the case, we need to look up and down and
see if there
are any end points. In this case, note how the graph has a upper
endpoint of y = -3 and it has arrows
going
down from that.
This means that the range is 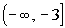 . . |
c) x-intercept
If the x-intercept
is where the graph crosses the x-axis,
what
do you think the x-intercept is for this
function?
If you said there is none, you are
right.
Since the graph never crosses the x-axis,
then there is no x-intercept. |
d) y-intercept
If the y-intercept is where the graph
crosses
the y-axis, what do you think the y-intercept
is for this function?
If you said y = -3 you
are correct.
The ordered pair for this y-intercept
would be (0, -3). |
e) Functional
value indicated
If the functional value correlates with the second or y value of an ordered pair what is f(-2)?
If you said f(-2) = -5 ,
then give yourself
a pat on the back. The functional value at x = -2 is -5.
The ordered pair for this would be (-2, -5). |
 Answer/Discussion
to 1b Answer/Discussion
to 1b
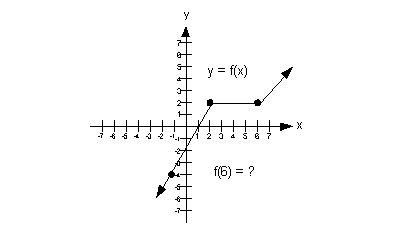
|
a) Domain
We need to find the set of all input values. In terms of ordered
pairs, that correlates with the first component of each one. In
terms
of this two dimensional graph, that corresponds with the x values
(horizontal axis).
Since that is the case, we need to look to the left and
right and see
if there are any end points. In this case, note how there are no
endpoints and the graph goes on and on forever in both
directions.
This means that the domain is 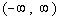 . . |
b) Range
We need to find the set of all output values. In terms of ordered
pairs, that correlates with the second component of each one. In terms
of this two dimensional graph, that corresponds with the y values (vertical axis).
Since that is the case, we need to look up and down and
see if there
are any end points. In this case, note how there are no endpoints
and the graph goes on and on forever in both directions.
This means that the range is 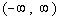 . . |
c) x-intercept
If the x-intercept
is where the graph crosses the x-axis,
what
do you think the x-intercept is for this
function?
If you said x = 1
you are correct.
The ordered pair for this x-intercept
would be (1, 0). |
d) y-intercept
If the y-intercept is where the graph
crosses
the y-axis, what do you think the y-intercept
is for this function?
If you said y = -2 you
are correct.
The ordered pair for this y-intercept
would be (0, -2). |
e) Functional
value indicated
If the functional value correlates with the second or y value of an ordered pair what is f(6)?
If you said f(6) = 2 ,
then give yourself
a pat on the back. The functional value at x = 6 is 2.
The ordered pair for this would be (6, 2). |
 Answer/Discussion
to 2a Answer/Discussion
to 2a
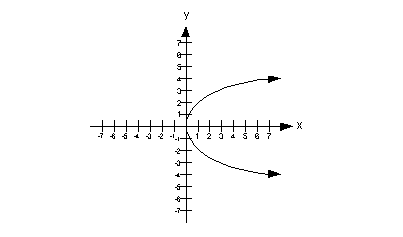
|
This graph would not pass the vertical line test
because there is at
least one place on it that we could draw a vertical line and intersect
it in more than one place. In fact, there are a lot of vertical
lines
that we can draw that would intersect it in more than one place, but we
only need to show one to say it is not a function.
The graph below shows one vertical line drawn through
our graph that
intersects it in two places: (1, 2) and (1, -2). This shows that
the input value of 1 associates with two output values, which is not
acceptable
in the function world.
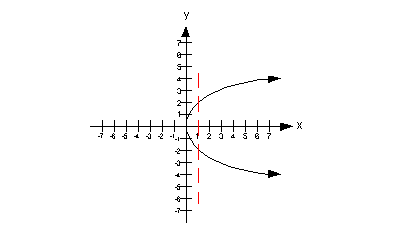
Therefore, this is not a graph of a function. |
 Answer/Discussion
to 2b Answer/Discussion
to 2b
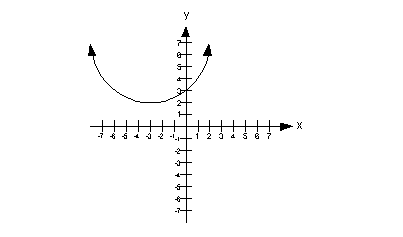
|
This graph would pass the vertical line test, because
there would not
be any place on it that we could draw a vertical line and it would
intersect
it in more than one place.
Therefore, this is a graph of a function. |
 Answer/Discussion
to 3a Answer/Discussion
to 3a
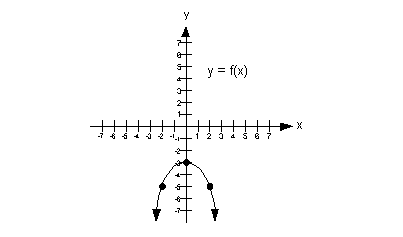
|
a) Increasing
A function is increasing in an interval when it is going up left to
right in that interval? With that in mind, what interval, if any,
is this function increasing?
If you said  ,
you are correct. ,
you are correct.
Note how the function is going up left to right, from
negative infinity
to x = 0.
Below shows the part of the graph that is increasing:
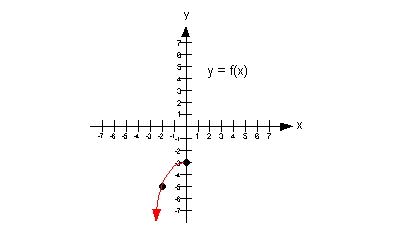
|
b) Decreasing
A function is decreasing in an interval when it is going down left
to right in that interval? With that in mind, what interval, if
any,
is this function decreasing?
If you said 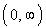 ,
you are right on. ,
you are right on.
Note how the function is going down left to right
starting at x =
0 and everywhere to the right of that.
Below shows the part of the graph that is decreasing:
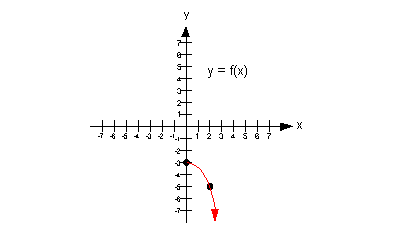
|
c) Constant
A function is constant in an interval if it is horizontal in the entire
interval. With that in mind, what interval, if any, is this
function
constant?
If you said it is never constant, pat yourself on the
back.
Note how the function is never a horizontal line. |
 Answer/Discussion
to 3b Answer/Discussion
to 3b
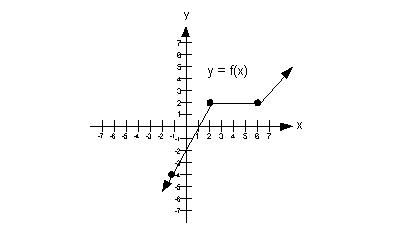
|
a) Increasing
A function is increasing in an interval when it is going up left to
right in that interval? With that in mind, what interval, if any,
is this function increasing?
If you said 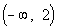 or or 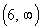 ,
you are correct. ,
you are correct.
Note how the function is going up left to right, from
negative infinity
to x = 2 and also starting at x = 6 and everywhere to the right of that.
Below shows the part of the graph that is increasing:
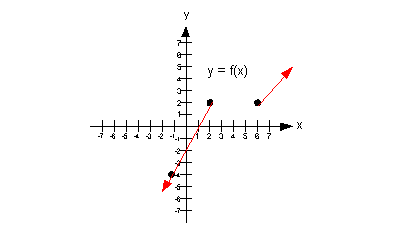
|
b) Decreasing
A function is decreasing in an interval when it is going down left
to right in that interval? With that in mind, what interval, if
any,
is this function decreasing?
If you said that it was never decreasing you are
right.
The graph never goes down left to right. |
c) Constant
A function is constant in an interval if it is horizontal in the entire
interval. With that in mind, what interval, if any, is this
function
constant?
If you said (2, 6), pat yourself on the back.
Note how the function is horizontal starting at x = 2 all the way to x = 6.
Below shows the part of the graph that is constant:
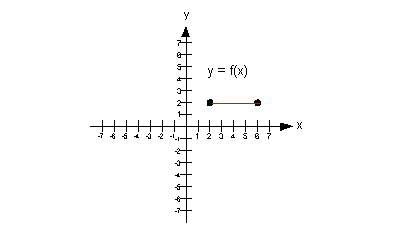
|
 Answer/Discussion
to 4a Answer/Discussion
to 4a
|
Note how this graph is symmetric about the y-axis:
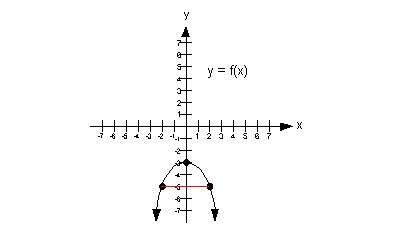
Do you know what that means?
It means that this function is even. |
 Answer/Discussion
to 4b Answer/Discussion
to 4b
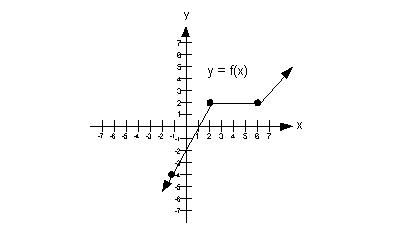
|
Note how the graph is neither symmetric about the y-axis
nor the origin.
Do you know what that means?
It means that this function is neither even nor odd. |
 Answer/Discussion
to 5a Answer/Discussion
to 5a
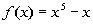
|
To determine if this function is even, odd, or
neither, we need
to replace x with -x and compare f(x)
with f(-x):
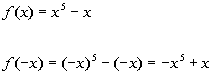
|
Even?
A function is even if 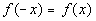 for all x in the domain of f.
With that in mind, is this function even? for all x in the domain of f.
With that in mind, is this function even?
If you said no, you are
correct. Note how
both of their terms have opposite signs, so 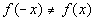 . . |
Odd?
A function is odd if 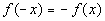 for all x in the domain of f.
With that in mind, is this function odd? for all x in the domain of f.
With that in mind, is this function odd?
If you said yes, you are
right.
Looking at 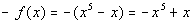 ,
note how all of the terms of f(-x)
and -f(x)
match up, so ,
note how all of the terms of f(-x)
and -f(x)
match up, so 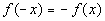 . .
Final answer: The function is
odd. |
 Answer/Discussion
to 5b Answer/Discussion
to 5b
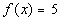
|
To determine if this function is even, odd, or
neither, we need
to replace x with -x and compare f(x)
with f(-x):
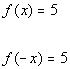
|
Even?
A function is even if 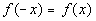 for all x in the domain of f.
With that in mind, is this function even? for all x in the domain of f.
With that in mind, is this function even?
If you said yes, you are
correct. Note how
all of the terms of f(x)
and f(-x) match up, so 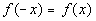 . .
Final answer: The function is
even. |
 Answer/Discussion
to 5c Answer/Discussion
to 5c
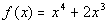
|
To determine if this function is even, odd, or
neither, we need
to replace x with -x and compare f(x)
with f(-x):
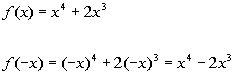
|
Even?
A function is even if 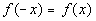 for all x in the domain of f.
With that in mind, is this function even? for all x in the domain of f.
With that in mind, is this function even?
If you said no, you are
correct. Note how
their second terms have opposite signs, so 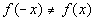 . . |
Since we said no for both even and odd, that leaves us
with our answer
to be neither.
Final answer: The function is neither even nor odd. |
 Answer/Discussion
to 6a Answer/Discussion
to 6a
f(-9.1) |
We need to ask ourselves, what is the greatest integer
that is less
than or equal to -9.1?
If you said -10, you are correct.
Be careful on this one. We are working with a
negative number.
-9 is not a correct answer because -9 is not less than or equal to
-9.1,
it is greater than -9.1.
Final answer: -10 |

Last revised on June 18, 2010 by Kim Seward.
All contents copyright (C) 2002 - 2010, WTAMU and Kim Seward. All rights reserved.
|
|


