Beginning Algebra Tutorial 20

Beginning Algebra
Tutorial 20: The Rectangular Coordinate System

WTAMU > Virtual Math Lab > Beginning Algebra

Learning Objectives

After completing this tutorial, you should be able to:

Plot points on a rectangular coordinate system.
Identify what quadrant or axis a point lies on.
Tell if an ordered pair is a solution of an equation in two variables or not.
Complete an ordered pair that has one missing value.

Introduction

This section covers the basic ideas of graphing: rectangular coordinate system, ordered pairs and solutions to equations in two variables. Graphs are important in giving a visual representation of the correlation between two variables. Even though in this section we are going to look at it generically, using a general x and y variable, you can use two-dimensional graphs for any application where you have two variables. For example, you may have a cost function that is dependent on the quantity of items made. If you needed to show your boss visually the correlation of the quantity with the cost, you could do that on a two-dimensional graph. I believe that it is important for you learn how to do something in general, then when you need to apply it to something specific you have the knowledge to do so. Going from general to specific is a lot easier than specific to general. And that is what we are doing here looking at graphing in general so later you can apply it to something specific, if needed.

Tutorial

Rectangular Coordinate System

The following is the rectangular coordinate system:

It is made up of two number lines:

The horizontal number line is the x- axis.
The vertical number line is the y- axis.

The origin is where the two intersect. This is where both number lines are 0.

It is split into four quadrants which are marked on this graph with Roman numerals.

Each point on the graph is associated with an ordered pair. When dealing with an x, y graph, the x coordinate is always first and the y coordinate is always second in the ordered pair (x, y). It is a solution to an equation in two variables. Even though there are two values in the ordered pair, be careful that it associates to ONLY ONE point on the graph, the point lines up with both the x value of the ordered pair (x-axis) and the y value of the ordered pair (y-axis).

Example 1: Plot the ordered pairs and name the quadrant or axis in which the point lies.
A(2, 3), B(-1, 2), C(-3, -4), D(2, 0), and E(0, 5).

Remember that each ordered pair associates with only one point on the graph. Just line up the x value and then the y value to get your location.

A(2, 3) lies in quadrant I.

B(-1, 2) lies in quadrant II.

C(-3, -4) lies in quadrant III.

D(2, 0) lies on the x-axis.

E(0, 5) lies on the y-axis.

Example 2: Find the x- and y- coordinates of the following labeled points

Remember that each ordered pair associates with only one point on the graph. Just line up the x value and then the y value to get your ordered pair.

Since point A corresponds to 2 on the x-axis and -3 on the y-axis, then A’s ordered pair is (2, -3).

Since point B corresponds to 3 on the x-axis and 2 on the y-axis, then B’s ordered pair is (3, 2).

Since point C corresponds to -2 on the x-axis and 3 on the y-axis, then C’s ordered pair is (-2, 3).

Since point D corresponds to -3 on the x-axis and - 4 on the y-axis, then D’s ordered pair is (-3, - 4).

Since point E corresponds to -3 on the x-axis and 0 on the y-axis, then E’s ordered pair is (-3, 0).

Since point F corresponds to 0 on the x-axis and 2 on the y-axis, then F’s ordered pair is (0, 2).

Solutions of Equations
in Two Variables

The solutions to equations in two variables consist of two values that when substituted into their corresponding variables in the equation, make a true statement.

In other words, if your equation has two variables x and y, and you plug in a value for x and its corresponding value for y and the mathematical statement comes out to be true, then the x and y value that you plugged in would together be a solution to the equation.

Equations in two variables can have more than one solution.

We usually write the solutions to equations in two variables in ordered pairs.

Example 3: Determine whether each ordered pair is a solution of the given equation.
y = 5x - 7; (2, 3), (1, 5), (-1, -12)

Let’s start with the ordered pair (2, 3).

Which number is the x value and which one is the y value? If you said x = 2 and y = 3, you are correct!

Let’s plug (2, 3) into the equation and see what we get:

*Plug in 2 for x and 3 for y

This is a TRUE statement, so (2, 3) is a solution to the equation y = 5x - 7.

Now let’s take a look at (1, 5).

Which number is the x value and which one is the y value? If you said x = 1 and y = 5, you are right!

Let’s plug (1, 5) into the equation and see what we get:

*Plug in 1 for x and 5 for y

Whoops, it looks like we have ourselves a FALSE statement. This means that (1, 5) is NOT a solution to the equation 5x - 7.

Now let’s look at (-1, -12).

Which number is the x value and which one is the y value? If you said x = -1 and y = -12, you are right!

Let’s plug (-1, -12) into the equation and see what we get:

*Plug in -1 for x and -12 for y

We have another TRUE statement. This means (-1, -12) is another solution to the equation y = 5x - 7.

Note that you were only given three ordered pairs to check, however, there are an infinite number of solutions to this equation. It would very cumbersome to find them all.

Example 4: Determine whether each ordered pair is a solution of the given equation.
x = 3; (3, 5), (2, 3), (3, 4)

This equation looks a little different than the one on example 3. In this equation, we only have an x value to plug in. So as long as the x value is 3, then we have a solution to the equation. It doesn’t matter what y’s value is.

Let’s start with the ordered pair (3, 5).

Which number is the x value and which one is the y value? If you said x = 3 and y = 5, you are correct!

Let’s plug (3, 5) into the equation and see what we get:

*Plug in 3 for x

This is a TRUE statement, so (3, 5) is a solution to the equation x = 3.

Now let’s take a look at (2, 3).

Which number is the x value and which one is the y value? If you said x = 2 and y = 3, you are right!

Let’s plug (2, 3) into the equation and see what we get:

*Plug in 2 for x

Whoops, it looks like we have ourselves a FALSE statement. This means that (2, 3) is NOT a solution to the equation x = 3.

Now let’s look at (3, 4).

Which number is the x value and which one is the y value? If you said x = 3 and y = 4, you are right!

Let’s plug (3, 4) into the equation and see what we get:

*Plug in 3 for x

We have another TRUE statement. This means (3, 4) is another solution to the equation x = 3.

Note that you were only given three ordered pairs to check, however, there are an infinite number of solutions to this equation. It would very cumbersome to find them all.

Finding the Corresponding Value in an Ordered Pair
Given One Variable’s Value

Again, the solutions to equations in two variables consist of two values that when substituted into their corresponding variables in the equation, make a true statement.

Sometimes you are given a value of one of the variables and you need to find the corresponding value of the other variable. The steps involved in doing that are:

Step 1: Plug given value for variable into equation.

Step 2: Solve the equation for the remaining variable.

Example 5: Complete each ordered pair so that it is a solution of the equation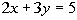

. (1, ) and ( , -1).

In the ordered pair (1, ), is 1 that is given the x or the y value?

If you said x, you are correct.

Plugging in 1 for x into the given equation and solving for y we get:

*Plug in 1 for x

*Solve for y

So, the ordered pair (1, 1) would be a solution to the given equation.

In the ordered pair ( , -1), is the -1 that is given the x or the y value?

If you said y, you are correct.

Plugging in -1 for y into the given equation and solving for x we get:

*Plug in -1 for y

*Solve for x

So, the ordered pair (4, -1) would be another solution to the given equation.

Example 6: Complete the table of values for the equation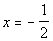

x y 0 -1 1

The only difference between this one and example 5 above is that we are using a table to match up our values of our variables instead of writing it in an ordered pair. The concept is still the same, we need to find the corresponding values of our variables that are solutions to the given equation.

Plugging in 0 for y into the given equation and solving for x we get:

So, the ordered pair (-1/2, 0) would be a solution to the given equation.

Plugging in -1 for y into the given equation and solving for x we get:

So, the ordered pair (-1/2, -1) would be another solution to the given equation.

Plugging in 1 for y into the given equation and solving for x we get:

So, the ordered pair (-1/2, 1) would be another solution to the given equation.

Filling in the table we get:

x y -1/2 0 -1/2 -1 -1/2 1

Practice Problems

�

These are practice problems to help bring you to the next level. It will allow you to check and see if you have an understanding of these types of problems. Math works just like anything else, if you want to get good at it, then you need to practice it. Even the best athletes and musicians had help along the way and lots of practice, practice, practice, to get good at their sport or instrument. In fact there is no such thing as too much practice.

To get the most out of these, you should work the problem out on your own and then check your answer by clicking on the link for the answer/discussion for that problem. At the link you will find the answer as well as any steps that went into finding that answer.

Practice Problem 1a: Plot each point and name the quadrant or axis in which the point lies.

1a. A(3, 1), B(-2, -1/2), C(2, -2), and D(0,1)
(answer/discussion to 1a)

Practice Problem 2a: Find the x- and y- coordinates of the following labeled points.

2a.

problem 2a

(answer/discussion to 2a)

Practice Problems 3a - 3b:Determine if each ordered pair is a solution of the given equation.

3a. y = 4x - 10 ; (0, -10), (1, -14), (-1, -14)
(answer/discussion to 3a)

3b. y = -5 ; (2, -5), (-5, 1), (0, -5)
(answer/discussion to 3b)

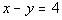Practice Problem 4a:Complete each ordered pair so that it is a solution of the equation .

4a. (0, ) and ( , 1).
(answer/discussion to 4a)

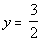Practice Problem 5a: Complete the table of values for the equation .

5a.

x y 0 -1 1

(answer/discussion to 5a)

Need Extra Help on these Topics?

The following is a webpage that can assist you in the topics that were covered on this page:

http://www.purplemath.com/modules/plane.htm
This webpage helps you with plotting points.

Go to Get Help Outside the Classroom found in Tutorial 1: How to Succeed in a Math Class for some more suggestions.

WTAMU > Virtual Math Lab > Beginning Algebra