Intermediate Algebra Tutorial 9

Intermediate Algebra
Answer/Discussion to Practice Problems
Tutorial 9: Formulas and Problem Solving

WTAMU > Virtual Math Lab > Intermediate Algebra > Tutorial 9: Formulas and Problem Solving

Answer/Discussion to 1a
I = PRT; for T

Do you recognize this formula?
This happens to be the formula for simple interest, where I = simple interest, P = principal, R = annual percentage rate, and T = time in years.

In this problem we need to solve for T. This means we need to get T on one side and EVERYTHING ELSE on the other side using inverse operations.

Let’s solve this formula for T:

*Inverse of mult. by PR is div. by PR

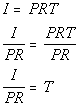
*Formula solved for T

(return to problem 1a)

Answer/Discussion to 1b
3x - 7y = 2; for y

In this problem we need to solve for y. This means we need to get y on one side and EVERYTHING ELSE on the other side using inverse operations.

Let’s solve this formula for y:

*Inverse of add 3x is sub. 3x

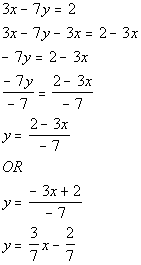
*Inverse of mult. by -7 is div. by -7

*Formula solved for y

*Divide num. by -7
*Another way to write it

(return to problem 1b)

Answer/Discussion to 2a
A principle of $50,000 is invested into a CD paying an annual percentage rate of 7.5%. Find the amount in the account after 10 years if the account is compounded monthly.

Step 1: Understand the problem.

Make sure that you read the question carefully several times.

Since we are looking for compound interest, we will need the compound interest formula:

The variables in this formula represent the following:

A = end amount in the account
P = principal (starting amount)
r = annual rate of interest
t = time in years
n = number of times compounded per year

Step 2: Devise a plan (translate).

In this problem,
A = ? = this is the variable we are looking for
P = 50000
r = 7.5% = .075
t = 10
n = 12 (There are 12 months in a year)

Plugging the values into the formula we get:

�

Step 3: Carry out the plan (solve).

*.075/12 = .00625 and 12(10) = 120

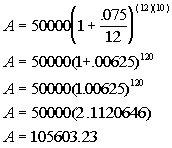
*Add inside the ( )
*Raise 1.00625 to the exponent of 120

*Multiply

Step 4: Look back (check and interpret).

If you take $50000 and compound it monthly for 10 years, you do end up with 105603.23

FINAL ANSWER: The compound amount is $105603.23.

(return to problem 2a)

Answer/Discussion to 2b
In Nebraska on I-80, the speed limit is 75 mph. How long would it take you to travel 525 miles in Nebraska on I-80 if you went the speed limit the whole time?

Step 1: Understand the problem.

Make sure that you read the question carefully several times.

Since we are looking for how long it would take you to travel, we can use the distance/rate formula:

d = rt

The variables in this formula represent the following:

d = distance
r = rate
t = time

Step 2: Devise a plan (translate).

In this problem,
d = 525
r = 75
t = = ? = this is the variable we are looking for

d = rt

Plugging the values into the formula we get:

Step 3: Carry out the plan (solve).

*Inverse of mult. by 75 is div. by 75

Step 4: Look back (check and interpret).

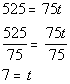
If you go at a rate of 75 miles per hour for 7 hours, you would travel 525 miles.

FINAL ANSWER: It would take 7 hours.

(return to problem 2b)

Answer/Discussion to 2c
Sally is training for the Olympics. She likes to run around a circular track that has a diameter of 60 yards, 20 times during a workout. How many yards does she run during her workout?

Step 1: Understand the problem.

Make sure that you read the question carefully several times.

Since we are needing to find the circumference of a circle, we can use this formula:

The variables in this formula represent the following:

C = circumference of a circle
r = radius

Step 2: Devise a plan (translate).

In this problem,
C = ? = this is the variable we are looking for
r = 30 (radius is half of the diameter, so r = 60/2 = 30)

Plugging the values into the formula we get:

Step 3: Carry out the plan (solve).

First, find the circumference of a circle.

*Multiply

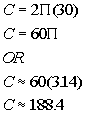
*Replace pi with 3.14 for an approximate value

For every workout, she runs around the track 20 times. So, we need to multiply the circumference by 20 to find the number of yards that she runs during her workout.

*Multiply

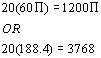
*Multiply using approx. value

Step 4: Look back (check and interpret).

If you take 2 times 30 you do get 60, so the circumference checks out. If you take 20 times 60 you do get 1200, so the number of yards ran in a workout checks out.

FINAL ANSWER: The number of yards that she runs in a workout is 1200 or approximately 3768.

(return to problem 2c)

WTAMU > Virtual Math Lab >Intermediate Algebra >Tutorial 9: Formulas and Problem Solving