Intermediate Algebra
Answer/Discussion to Practice Problems
Tutorial 6: Practice Test on Tutorials 2 - 5
Problems 1a - 1b: Find the value of the algebraic expression
at the given replacement values. |
1a. x + y when x = 5.2 and y = 3.9
 Answer: Answer:
In this problem, we will be replacing x with
5.2 and y with 3.9:
x + y =
5.2 + 3.9 =
9.1 |
1b. If it costs $450 per tv at a local entertainment store, then
we can use the algebraic expression 450x, where x represents the number of tv's purchased, to find the cost of buying x tv's. How much would it cost to buy 3?
 Answer: Answer:
In this problem we will be replacing x with 3 and multiplying it times 450.
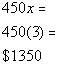
|
Problems 2a - 2b: Write the phrase as an algebraic expression. |
2a. The product of a 12 and a number.
 Answer: Answer:
Product will be substituted with multiplication and we will replace
the phrase 'a number' with the variable x.
Putting it all together we get:
The product of 12 and a number
12x
|
2b. The quotient of 25 and the difference of a number and 3.
 Answer: Answer:
Quotient is the same as divide, difference will be translated as subtraction
and we will replace the phrase 'a number' with the variable x.
Putting it all together we get:
The quotient of 25 and the difference of a number and 3.
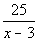
|
Problems 3a - 3c: List the elements of each set. |
3a. {x | x is a natural number between 10 and 20}
 Answer: Answer:
There are two parts to this:
- the number has to belong to the set of natural numbers {1, 2, 3, 4, ...}
and
- it has to be between 10 and 20.
Putting these two ideas together we get:
{11, 12, 13, 14, 15, 16, 17, 18, 19}
|
3b. {x | x is a whole number greater than 5}
 Answer: Answer:
There are two parts to this:
- the number has to belong to the set of whole numbers {0, 1, 2, 3, 4, ...}
and
- it has to be greater than 5.
Putting these two ideas together we get:
{6, 7, 8, 9, ...}
|
3c. {x | x is a whole number less than 10}
 Answer: Answer:
There are two parts to this:
- the number has to belong to the set of whole numbers {0, 1, 2, 3, 4, ...}
and
- it has to be less than 10.
Putting these two ideas together we get:
{0, 1, 2, 3, 4, 5, 6, 7, 8, 9}
|
Problem 4a: Graph the set on a number line. |
4a {-3, -2.5, 0, 3/2, 3}
 Answer: Answer:
Note that -2.5 goes halfway between -2 and -3.
Also note that 3/2 = 1.5 and goes halfway between 1 and 2.
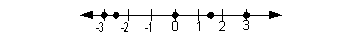
|
Problems 5a - 5f : List the elements of the following set
that are also elements of the given set.
|
5a. Natural numbers:  Answer: Answer:
{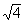 } }
|
5b. Whole numbers:  Answer: Answer:
{0, 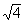 } }
|
5c. Integers:  Answer: Answer:
{-5, 0, 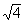 } }
|
5d. Rational numbers:  Answer: Answer:
{-5, -2.5, 0,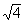 } }
|
Problems 6a - 6b: Place 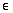 or or 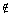 to make
each statement true. to make
each statement true. |
6a. 0 ? {x | x is
a natural number}
 Answer: Answer:
Since 0 is NOT one of our counting numbers, then it would be true to
say:
0 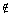 {x | x is a natural number} {x | x is a natural number}
|
6b. .25 ? {x | x is a rational number}
 Answer: Answer:
Since .25 can be written as 1/4 (one integer over another), it would
be true to say:
.25 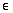 {x | x is a rational number} {x | x is a rational number}
|
Problems 7a - 7b: Determine whether the statement is true
or false. |
7a. 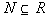
 Answer: Answer:
Since EVERY element of N (natural numbers)
is also in R (Real numbers), then this statement
is TRUE.
|
7b. 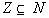
 Answer: Answer:
Since not EVERY element of Z (integers)
is in N (natural numbers), then this statement
is FALSE.
|
Problems 8a - 8c: Find the absolute value. |
8a. |4.2|
 Answer: Answer:
Since 4.2 is 4.2 units away from 0 on the number line,
|4.2| = 4.2 |
8b. |- 4.2|
 Answer: Answer:
Since - 4.2 is 4.2 units away from 0 on the number line,
|- 4.2| = 4.2 |
8c. -|20|
 Answer: Answer:
Putting together the facts that 20 is 20 units away from the origin
and there is a negative IN FRONT of the absolute value we get
-|20| = -20 |
Problems 9a - 9b: Find the sum or difference. |
9a. -35 + (-15)
 Answer: Answer:
-35 + (-15) = -50
Note that we are adding two numbers with the same sign. The sum
of the absolute values 35 and 15 is 50 and their common sign is negative.
Therefore, our answer is -50.
Thinking in terms of money: You lost 35 dollars and then you lost another
15 dollars, so you lost a total of 50 dollars. |
9b. -14 - (-5)
 Answer: Answer:
-14 - (-5) = -14 + 5 = -9
Subtracting a negative 5 is the same as adding a positive 5. Once
we change it to addition, we now are adding two numbers with opposite signs.
The difference of the absolute values of 14 and 5 is 9 and the sign of
the larger absolute value (-14) is negative. Therefore, our answer is
-9.
Thinking in terms of money: You are in the hole 14 dollars, then you
gain 5 dollars, you are still in the hole 9 dollars. |
Problems 10a - 10b: Find the product or quotient |
10a. (-15)(-10)
 Answer: Answer:
(-15)(-10) = 150
We are multiplying two numbers with the same sign. The product
of 15 and 10 is 150 and multiplying with same signs gives us a positive
answer. Therefore, our answer is 150. |
10b. 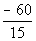
 Answer: Answer:
-60/15 = - 4
We are dividing two numbers with opposite signs. The quotient
of -60 and 15 is 4 and dividing with opposite signs gives us a negative.
Therefore, our answer is -4. |
Problems 11a - 11b: Evaluate. |
11a. 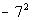
 Answer: Answer:
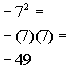
|
11b. 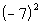
 Answer: Answer:
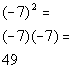
|
Problems 12a - 12b: Find the root. |
12a. 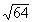
 Answer: Answer:
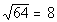
The square root of 64 is 8, since 8 squared is 64. |
12b. 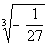
 Answer: Answer:
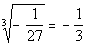
The CUBE root of -1/27 is -1/3 since -1/3, cubed is -1/27. |
Problems 13a - 13b: Simplify. |
Problem 14a: Find the value of the expression when a = 5 and b = -3. |
14a. -6(2a - 3b)
 Answer: Answer:
Replacing a with 5 and b with -3 and evaluating the expression we get,
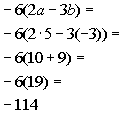
|
Problems 15a - 15b: Write the opposite (additive inverse)
and the reciprocal (multiplicative inverse) of each number. |
15a. 10
 Answer: Answer:
The opposite of 10 is -10, since 10 + (-10) = 0.
The reciprocal of 10 is 1/10, since 10(1/10) = 1. |
15b. -1/2
 Answer: Answer:
The opposite of -1/2 is 1/2, since -1/2 + 1/2 = 0.
The reciprocal of -1/2 is -2, since (-1/2)(-2) = 1. |
Problems 16a - 16b: Use a commutative property to write an equivalent
expression. |
16a. 5 + b
 Answer: Answer:
Using the commutative property of addition (where changing the order
of a sum does not change the value of it) we get:
5 + b = b + 5
|
16b. 7a
 Answer: Answer:
Using the commutative property of multiplication (where changing the
order of a product does not change the value of it) we get:
7a = a7
|
Problems 17a - 17b: Use an associative property to write an
equivalent expression. |
17a. (-10a)b
 Answer: Answer:
Using the associative property of multiplication (where changing the
grouping of a product does not change the value of it) we get:
(-10a)b = -10(ab)
|
17b. x + (2y + 3z)
 Answer: Answer:
Using the associative property of addition (where changing the grouping
of a sum does not change the value of it) we get
x + (2y +
3z) = (x + 2y)
+ 3z
|
Problems 18a - 18b: Use the distributive property to find
the product. |
18a. -(5a - 6b)
 Answer: Answer:
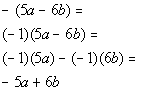
|
18b. 3(2x + 4y + 5z)
 Answer: Answer:
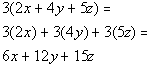
|
Problem 19a: Simplify the expression. |
19a. 3(a - 4) + 4(a + 5)
 Answer: Answer:
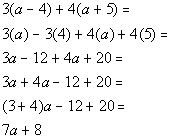
|
Problems 20a - 20b: Write each statement using mathematical symbols. |
20a. The sum of x and 5 is less than
or equal to the opposite of 9.
 Answer: Answer:
Sum translates into addition.
Is less than or equal to will need to be replaced by the symbol <.
The opposite of 9 is -9.
Let's put everything together going left to right:
The sum of x and 5 is less than or equal to the opposite of 9.
x + 5 < -9
|
20b. Twice the difference of y and
6 is not equal to the reciprocal of 1/5.
 Answer: Answer:
Twice translates as 2 times and difference is the same as subtraction.
Is not equal to will need to be replaced by the symbol 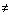 . .
The reciprocal of 1/5 is 5.
Let's put everything together going left to right:
Twice the difference of y and 6 is not
equal to the reciprocal of 1/5.
2(y - 6) 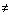 5 5
|
Problem 21a: Write the following as an algebraic expression. |
21a. The cost of x hamburgers,
if each hamburger costs $1.75.
 Answer: Answer:
If each hamburger costs 1.75, then in order to find the cost, we would
have to multiply the number of hamburgers (x)
by the cost per hamburger (1.75).
Hence, we would get the algebraic expression 1.75x. |
Problems 22a - 22c: Insert <, > , or = to form a true statement. |
22a. 1.5 ? 3/2
 Answer: Answer:
Since 3/2 simplifies to 1.5, then 1.5 equals 3/2:
1.5 = 3/2
|
22b. -3 ? -1
 Answer: Answer:
Since -3 is to the left of -1 on the number line, then -3 is less than
-1:
-3 < -1
|
22c. 0 ? -5
 Answer: Answer:
Since 0 is to the right of -5 on the number line, then 0 is greater
than - 5:
0 > -5
|

Last revised on June 17, 2011 by Kim Seward.
All contents copyright (C) 2002 - 2011, WTAMU and Kim Seward.
All rights reserved.
|
|


