Intermediate Algebra
Tutorial 3: Sets of Numbers
|
WTAMU > Virtual Math Lab > Intermediate Algebra
 Learning Objectives Learning Objectives
After completing this tutorial, you should be able to:
- Graph a point on a real number line.
- Know what a set and an element are.
- Indicate if something is an element or is not an element of a set, using
the appropriate notation.
- Tell if one set is a subset of another set.
- Read or write out a set in either roster form or set builder form.
- Know what the empty set is and how to notate it.
- Identify what numbers belong to the set of natural numbers, whole numbers,
integers, rational numbers, irrational numbers, and real numbers.
- Find the absolute value of a number.
- Find the opposite of a number.
|
 Introduction Introduction
Have you ever sat in a math class, and you swear the teacher is speaking
some foreign language? Well, algebra does have it's own lingo.
This tutorial will go over some key definitions and phrases used when specifically
working with sets of numbers as well as absolute values and opposites.
Even though it may not be the exciting part of math, it is very important
that you understand the language spoken in algebra class. It will
definitely help you do the math that comes later. Of course, numbers
are very important in math. This tutorial helps you to build an understanding
of what the different sets of numbers are. You will also learn
what set(s) of numbers specific numbers, like -3, 0, 100, and even 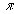
(pi) belong to. Some of them belong to
more than one set. I think you are ready to go forward. Let's
make you a numeric set whiz kid (or adult). |
 Tutorial Tutorial
|
Real Number Line
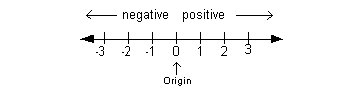
|
Above is an illustration of a number line. Zero, on the number
line, is called the origin. It separates the negative numbers
(located to the left of 0) from the positive numbers (located to
the right of 0).
I feel sorry for 0, it does not belong to either group. It is
neither a positive or a negative number.
When graphing a point on the number line, you simply color in a point
that corresponds to that number on the number line as illustrated below.
That is how you graph a solution on the number line.
This is how you would graph it if your solution was the number 2:

|
A set is a collection of objects.
Those objects are generally called elements of the set.
The symbol 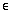 means 'is an element of.'
means 'is an element of.'
So, it stands to reason that 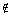 represents 'is not an element of.'
represents 'is not an element of.' |
We say that A is a subset of B, written A 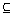 B, when every element of A is contained in B.
(It does not necessarily mean that every element of B is also contained
in A) |
There are several ways to notate a set, the two most common ways
are:
- the roster form and
- set builder notation.
|
Roster form just lists out the elements of a set between two set
brackets. For example,
{January, June, July}
Set builder notation describes the members of the set without listing
them. It is also written between two set brackets.
For example,
{x | x is a
month that begins with J}
When writing it in set builder notation you always do the following: start off with a left set bracket, then you put x followed by a vertical
bar which is interpreted as 'such that'. Then you write out the description
of the elements of the set. Finish it with a right set bracket.
So the above illustration would be read: "x,
such that, x is a month that begins with J."
It is important to know set builder notation, especially in mathematics,
because it allows you to group together large number of elements that belong
to a certain category. The above set has only 3 elements, so it would
not be difficult to write it in roster form as shown above. However,
if your set has hundreds or thousands of elements, it would be hard to
list them out, but easy to refer to them using set builder notation.
For example, {x| x is a college student in Texas}.
Before we move on to the math aspect of sets, there is one more term
we need to make sure you have a handle on. |
Empty (or null) set is a set that contains no elements.
It is symbolized by { } OR 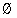 . .
Be careful. It is real tempting to use them together, but {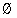 }
IS NOT a way to indicate empty set. }
IS NOT a way to indicate empty set.
Let's move on to some special sets that pertain specifically to math.
Note that the three dots shown in the sets below are called ellipsis.
It indicates that the elements in the set would continue in the same
pattern. - In other words, the list would keep going and going in that
direction using the pattern illustrated. |
|
Natural (or Counting) Numbers
N = {1, 2, 3, 4, 5, ...}
|
Makes sense, we start counting with the number 1 and continue with
2, 3, 4, 5, and so on. |
|
Whole Numbers
{0, 1, 2, 3, 4, 5, ...}
|
The only difference between this set and the one above is that this
set not only contains all the natural numbers, but it also contains 0, where as 0 is not an element of the set of natural numbers. |
|
Integers
Z = {..., -5, -4, -3, -2, -1, 0, 1, 2, 3, 4,
5, ...}
|
This set adds on the negative counterparts to the already existing
whole numbers (which, remember, includes the number 0).
The natural numbers and the whole numbers are both subsets of integers. |
|
Rational Numbers
Q = {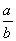 |
a and b are integers and |
a and b are integers and 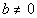 } }
|
In other words, a rational number is a number that can be written
as one integer over another.
Be very careful. Remember that a whole number
can be written as one integer over another integer. The integer
in the denominator is 1 in that case. For example, 5 can be written as
5/1.
The natural numbers, whole numbers, and integers are all subsets
of rational numbers. |
|
Irrational Numbers
I = {x | x is a real number that
is not rational}
|
In other words, an irrational number is a number that can not be written
as one integer over another. It is a non-repeating, non-terminating
decimal.
One big example of irrational numbers is roots of numbers that are
not perfect roots - for example 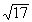 or or 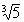 .
17 is not a perfect square - the answer is a non-terminating,
non-repeating decimal, which CANNOT be written as one integer over another.
Similarly, 5 is not a perfect cube. It's answer is also a non-terminating,
non-repeating decimal. .
17 is not a perfect square - the answer is a non-terminating,
non-repeating decimal, which CANNOT be written as one integer over another.
Similarly, 5 is not a perfect cube. It's answer is also a non-terminating,
non-repeating decimal.
Another famous irrational number is 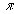 (pi). Even though it is more commonly known as 3.14, that is
a rounded value for pi. Actually it is 3.1415927... It would keep
going and going and going without any real repetition or pattern. In other
words, it would be a non terminating, non repeating decimal, which again,
can not be written as a rational number, 1 integer over another integer.
(pi). Even though it is more commonly known as 3.14, that is
a rounded value for pi. Actually it is 3.1415927... It would keep
going and going and going without any real repetition or pattern. In other
words, it would be a non terminating, non repeating decimal, which again,
can not be written as a rational number, 1 integer over another integer. |
|
Real Numbers
R = {x | x corresponds to point
on the number line}
|
Any number that belongs to either the rational numbers or irrational
numbers would be considered a real number. That would include natural numbers,
whole numbers and integers.
 Example
1: List the elements of the set {x | x is a whole number less than 11} Example
1: List the elements of the set {x | x is a whole number less than 11}
|
There are two parts to this:
- the number has to belong to the set of whole numbers {0, 1, 2, 3, ...}
and
- it has to be less than 11.
Putting these two ideas together we get:
{0, 1, 2, 3, ..., 9, 10}
|
 Example
2: Example
2: List the elements of the set { x | x is a natural number between 5 and 11}. |
There are two parts to this:
- the number has to belong to the set of natural numbers {1, 2, 3, ...}
and
- it has to be between 5 and 11 - which by the way would not include those
two numbers.
Let's see what we get when we put those ideas together:
{6, 7, 8, 9, 10}
You would not have an ellipsis after the 10 because this set would stop
at the number 10. |
 Example
3: Example
3: List the elements of the set { x | x is a natural number greater than 100}. |
There are two parts to this:
- the number has to belong to the set of natural numbers {1, 2, 3, ...}
and
- it has to be greater than 100.
Let's see if you figured this one out ok:
{101, 102, 103, 104, ...}
Did you remember to include the ellipsis to show that the set would
continue on and on in the same pattern? |
 Example
4: Example
4: Graph the set on a number line.
{-2, -.5, 0, 1/5, 3} |
When you graph fractions or decimals, you need to first figure out
between what two integers it belongs and then estimate, depending
on the fraction, where you are going to place the point between those two
numbers.
In this problem, we have a -.5, which is between -1 and 0. Since
it is halfway between these two numbers, I would place the dot halfway
between.
We also have the fraction 1/5, which is between 0 and 1 and since it
is closer to 0 than 1, I would place it accordingly on the graph.
The other numbers are integers that are already marked clearly on the
graph.
Let's see what we get when we graph all of these real numbers:
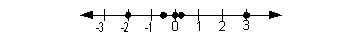
|
 Example
5: Example
5: List the elements of the following sets that
are also elements of the given set
{-4, 0, 2.5, 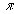 , , 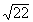 , , 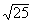 ,
11/2, 7} ,
11/2, 7}
Natural numbers, whole numbers, integers, rational numbers, irrational
numbers, and real numbers. |
|
{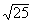 , 7}. , 7}.
Note that 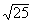 simplifies
to be 5, which is a natural number. simplifies
to be 5, which is a natural number. |
Whole numbers?
The numbers in the given set that are also whole numbers are
{0, 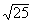 , 7}. , 7}.
|
Integers?
The numbers in the given set that are also integers are
{-4, 0,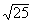 , 7}. , 7}.
|
|
{-4, 0, 2.5,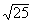 , 11/2,
7}. , 11/2,
7}.
|
|
{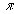 , , 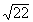 }. }.
These two numbers CANNOT be written as one integer over another.
They are non-repeating, non-terminating decimals. |
Real numbers?
The numbers in the given set that are also real numbers are
{-4, 0, 2.5, 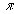 , , 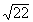 , ,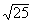 ,
11/2, 7}. ,
11/2, 7}.
|
 Example
6: Example
6: Place a 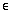 or 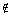 to make the statement true.
0 ? {x | x is
a whole number} |
Since 0 is one of the elements listed in the set of whole
numbers, then it would be true to say
0 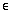 {x | x is a whole
number}.
{x | x is a whole
number}.
|
 Example
7: Example
7: Place a 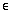 or 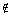 to make the statement true.
-2 ? {2, 4, 6, .... } |
Since -2 is not listed and the ellipsis would indicate listing out
more positive even numbers, it looks like -2 is not part of this set.
Therefore, it would be a true statement to say
-2 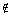 {2,
4, 6, .... }. {2,
4, 6, .... }.
|
 Example
8: Example
8: Place a 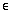 or 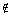 to make the statement true.
½ ? {x | x is an irrational number} |
|
½ 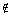 {x | x is an irrational
number}. {x | x is an irrational
number}.
|
 Example
9: Example
9: Place a 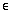 or 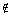 to make the statement true.
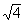 ?
{x | x is a rational
number} ?
{x | x is a rational
number}
|
Since 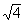 simplifies
to be 2, which can be written as 2/1, we can write the following true statement
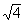 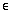 {x | x is a rational
number}.
{x | x is a rational
number}.
|
 Example
10: Example
10: Determine if the statement is true or false?
N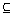 I I |
|
In fact, there are no elements in N that
are in I. |
 Example
11: Example
11: Determine if the statement is true or false? I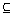 R R |
 Example
12: Example
12: Determine if the statement is true or false?
N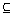 Q Q |
Most people know that when you take the absolute value of ANY number
(other than 0) the answer is positive. But, do you know WHY?
Well, let me tell you why!
The absolute value of x, notated |x|,
measures the DISTANCE that x is away from the
origin (0) on the real number line.
Aha! Distance is always going to be positive (unless it is 0)
whether the number you are taking the absolute value of is positive or
negative.
The following are illustrations of what absolute value means using
the numbers 3 and -3:
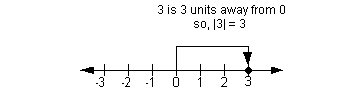
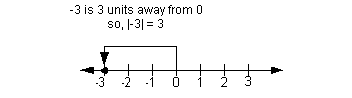
 Example
13: Find the absolute value.
|-7| Example
13: Find the absolute value.
|-7|
|
When looking for the absolute value of -7, we are looking for the number
of units (or distance) -7 is from 0 on the number line.
I came up with 7, how about you? |
 Example
14: Example
14: Find the absolute value. |7| |
When looking for the absolute value of 7, we are looking for the number
of units (or distance) 7 is from 0 on the number line.
I came up with 7, how about you? |
 Example
15: Example
15: Find the absolute value.
- |-2| |
This problem has a little twist to it. Let's talk it through.
First of all, if we just concentrate on |-2|, we would get 2.
Second, note that there is a negative on the OUTSIDE of the absolute
value. That means we are going to take the
opposite of what we get for the absolute value.
Putting that together we get -2 for our answer.
Note that the absolute value part of the problem was still positive.
We just had a negative on the outside of it that made the final answer
negative. |
Opposites are two numbers that are on opposite sides of the origin
(0) on the number line, but have the same absolute value. In other words, opposites are the same distance away from the origin, but
in opposite directions.
The opposite of x is the number -x.
Keep in mind that the opposite of 0 is 0.
The following is an illustration of opposites using the numbers 3
and -3:
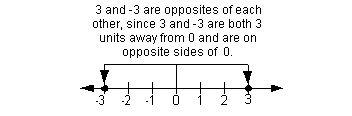
|
The double negative property reads that for every real number a,
-(-a) = a.
When you see a negative sign in front of an expression, you can think
of it as taking the opposite of it. For example, if you had -(-2),
you can think of it as the opposite of -2. Since a number can only
have one of two signs, either a '+' or a '-', then the opposite of a negative
would have to be positive. So, -(-2) = 2.
 Example
16: Write the opposite of 1.5. Example
16: Write the opposite of 1.5.
|
The opposite of 1.5 is -1.5, since both of these numbers have
the same absolute value but are on opposite sides of the origin on the
number line. |
 Example
17: Example
17: Write the opposite of -3. |
The opposite of -3 is 3, since both of these numbers have the
same absolute value but are on opposite sides of the origin on the number
line. |
 Practice Problems Practice Problems
These are practice problems to help bring you to the
next level.
It will allow you to check and see if you have an understanding of
these
types of problems. Math works just like
anything
else, if you want to get good at it, then you need to practice
it.
Even the best athletes and musicians had help along the way and lots of
practice, practice, practice, to get good at their sport or instrument.
In fact there is no such thing as too much practice.
To get the most out of these, you should work the
problem out on
your own and then check your answer by clicking on the link for the
answer/discussion
for that problem. At the link you will find the answer
as well as any steps that went into finding that answer. |
 Practice
Problems 1a - 1c: List the elements of each set. Practice
Problems 1a - 1c: List the elements of each set.
 Practice
Problem 2a: Graph the set on a number line. Practice
Problem 2a: Graph the set on a number line.
 Practice
Problems 3a - 3f: List the elements of the following set that are also
elements of the given set: {-1.5, 0, 2, Practice
Problems 3a - 3f: List the elements of the following set that are also
elements of the given set: {-1.5, 0, 2,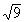 , , 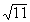 } }
 Practice
Problems 4a - 4c: Place Practice
Problems 4a - 4c: Place 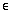 or or 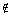 to make
each statement true. to make
each statement true.
 Practice
Problems 5a - 5b: Determine whether the statement
is true or false. Practice
Problems 5a - 5b: Determine whether the statement
is true or false.
 Practice
Problems 6a - 6b: Find the absolute value. Practice
Problems 6a - 6b: Find the absolute value.
 Practice
Problems 7a - 7b: Write the opposite of the number. Practice
Problems 7a - 7b: Write the opposite of the number.
 Need Extra Help on these Topics? Need Extra Help on these Topics?

Last revised on June 10, 2011 by Kim Seward.
All contents copyright (C) 2002 - 2011, WTAMU and Kim Seward. All rights reserved.
|


