---

 

Answer/Discussion to 1a

 

Step 1: Find the LCD if needed.

 

The first denominator has the following factor:

 
 

The second denominator, 5 - x, looks like the first denominator except the signs are switched.  We can rewrite this as

 

*Factor out a -1

 

Putting all the different factors together and using the highest exponent, we get the following LCD:

 
 

Note that I did not put the -1 that was in front of the second denominator's (x - 5) factor.  In the step 3, I will put the negative into the problem by placing it in the numerator of that second fraction.

 

Step 2: Write equivalent fractions using the LCD if needed.

 

Now the two fractions have a common denominator, so we do not have to rewrite the rational expressions.

 
 

Step 3: Combine the rational expressions.

 

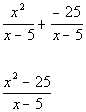
*Combine the two num. *Write over the common den.

 

Step 4: Reduce to lowest terms as shown in Tutorial 32: Multiplying and Dividing Rational Expressions.

 

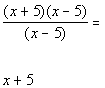
*Factor the diff. of two squares in the num.     *Divide out the common factor of (x - 5)

 

(return to problem 1a)

 

 

Answer/Discussion to 1b

 

Step 1: Find the LCD if needed.

 

The first denominator has the following factors:

 

*Factor the trinomial

 

The second denominator has the following factor:

 
 

Putting all the different factors together and using the highest exponent, we get the following LCD:

 
 

Step 2: Write equivalent fractions using the LCD if needed.

 

Since the first rational expression already has the LCD, then we do not need to change this fraction.

 

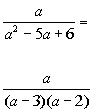
*Rewriting denominator in factored form

 

Rewriting the second expression with the LCD:

 

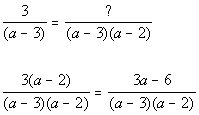
*Missing the factor of (a - 2) in the den. *Mult. top and bottom by (a - 2)

 
 

Step 3: Combine the rational expressions.

 

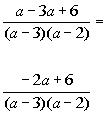
*Combine the two num. *Write over the common den.

 

Step 4: Reduce to lowest terms, as shown in Tutorial 32: Multiplying and Dividing Rational Expressions.

 

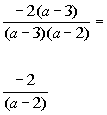
*Factor out a GCF of -2 in num.     *Divide out the common factor of (a - 3)

 

(return to problem 1b)

 

 
 

Answer/Discussion to 1c

 

Step 1: Find the LCD if needed.

 

The first denominator has the following factor:

 
 

The second denominator has the following factors:

 

*Factor out a GCF of 2

 

The third denominator has the following factors:

 

*Factor out a GCF of x

 

Putting all the different factors together and using the highest exponent, we get the following LCD:

 
 

Step 2: Write equivalent fractions using the LCD if needed.

 

Rewriting the first expression with the LCD:

 

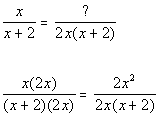
*Missing the factors 2 and x in the den.   *Mult. top and bottom by 2x

 

Rewriting the second expression with the LCD:

 

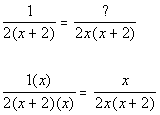
*Missing the factor of x in the den. *Mult. top and bottom by x

 

Rewriting the third expression with the LCD:

 

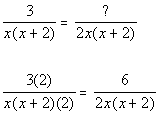
*Missing the factor of 2 in the den. *Mult. top and bottom by 2

 

Step 3: Combine the rational expressions.

 

*Combine the three num. *Write over the common den.

 

Step 4: Reduce to lowest terms, as shown in Tutorial 32: Multiplying and Dividing Rational Expressions.

 

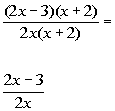
*Factor the trinomial in num.     *Divide out the common factor of (x + 2)

 

(return to problem 1c)

 

---

Last revised on July 17, 2011 by Kim Seward.
All contents copyright (C) 2001 - 2011, WTAMU and Kim Seward. All rights reserved.