Intermediate Algebra Tutorial 29


Intermediate Algebra
Answer/Discussion to Practice Problems
Tutorial 29: Factoring Special Products

WTAMU > Virtual Math Lab > Intermediate Algebra > Tutorial 29: Factoring Special Products


 

checkAnswer/Discussion to 1a

problem 1a
 

First note that there is no GCF to factor out of this polynomial. 

Since it is a trinomial, you can try factoring this by trial and error as shown in Tutorial 28: Factoring Trinomials.  But if you can recognize that it fits the form of a  perfect square trinomial, you can save yourself some time.
 

ad1a

*Fits the form of a perfect sq. trinomial
*Factor as the sum of bases squared

 
There is no more factoring that we can do in this problem.

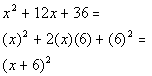
Note that if we would multiply this out, we would get the original polynomial.
 

(return to problem 1a)

 


 

checkAnswer/Discussion to 1b

problem 1b
 

The first thing that we always check when we are factoring is WHAT?

The GCF.  In this case, there is one. 

Factoring out the GCF of 2 as was shown in Tutorial 27: The GCF and Factoring by Grouping, we get:
 

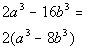
ad1b1

*Factor out the GCF of 2

 
This fits the form of the difference of cubes.  So we will factor using that rule:

 
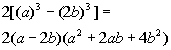
ad1b2
*Fits the form of a diff. of two cubes
*Binomial is diff. of bases
*Trinomial is 1st base squared, plus prod. of bases, plus 2nd base squared

 
There is no more factoring that we can do in this problem.

Note that if we would multiply this out, we would get the original polynomial.
 

(return to problem 1b)


 

checkAnswer/Discussion to 1c

problem 1c
 

The first thing that we always check when we are factoring is WHAT?

The GCF.  In this case, there is one. 

Factoring out the GCF of 5 as was shown in Tutorial 27: The GCF and Factoring by Grouping, we get:
 

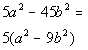
ad1c1

*Factor out the GCF of 5

 
This fits the form of the difference of squares.  So we will factor using that rule:

 
ad1c2
*Fits the form of a diff. of two squares
*Factor as the prod. of sum and diff. of bases

 
There is no more factoring that we can do in this problem.

Note that if we would multiply this out, we would get the original polynomial.
 

(return to problem 1c)

 


 

checkAnswer/Discussion to 1d

problem 1d
 

First note that there is no GCF to factor out of this polynomial. 

This is a polynomial with four terms.  Looks like we will have to try factoring it by grouping as shown in Tutorial 27:  The Greatest Common Factor and Factoring by Grouping:
 

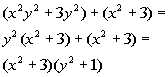
ad1d1

*Group in two's
*Factor out the GCF out of each separate (   )
*Factor out the GCF of (x squared + 3)

 
There is no more factoring that we can do in this problem.

Note that if we would multiply this out, we would get the original polynomial.
 

(return to problem 1d)

 


 

checkAnswer/Discussion to 1e

problem 1e
 

First note that there is no GCF to factor out of this polynomial. 

This is a trinomial that does not fit the form of a perfect square trinomial.  Looks like we will have to use trial and error as shown in Tutorial 28: Factoring Trinomials:
 

ad1e1

*Factor by trial and error

 
There is no more factoring that we can do in this problem.

Note that if we would multiply this out, we would get the original polynomial.
 

(return to problem 1e)

 

Buffalo Top

 
WTAMU > Virtual Math Lab >Intermediate Algebra >Tutorial 29: Factoring Special Products


Last revised on July 15, 2011 by Kim Seward.
All contents copyright (C) 2001 - 2011, WTAMU and Kim Seward. All rights reserved.