Answer/Discussion on Factoring Trinomials

(Back to the tutorial on factoring trinomials)

Intermediate Algebra
Answer/Discussion to Practice Problems
on Factoring Trinomials

Answer/Discussion to 1a

Note that this trinomial does not have a GCF.

So we go right into factoring the trinomial of the form

Step 1: Set up a product of two ( ) where each will hold two terms.

It will look like this: ( )( )

Step 2: Find the factors that go in the first positions.

Since we have x squared as our first term, we will need the following:

(x )(x )

Step 3: Find the factors that go in the last positions.

We need two numbers whose product is -14 and sum is 5. That would have to be 7 and -2.

Putting that into our factors we get:

*7 and -2 are two numbers whose prod. is -14
and sum is 5

Note that if we would multiply this out we would get the original trinomial.

(return to problem 1a)

Answer/Discussion to 1b

Note that this trinomial does have a GCF of 3b.

We need to factor out the GCF, as shown in Tutorial 27: The GCF and Factoring by Grouping, first before we tackle the trinomial part of this.

*Factor out the GCF of 3b

We are not finished, we can still factor the trinomial. It is of the form

Step 1: Set up a product of two ( ) where each will hold two terms.

It will look like this: ( )( )

Step 2: Use trial and error to find the factors needed.

In the first terms of the binomials, we need factors of 2 a squared. This would have to be 2a and a.

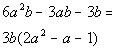
In the second terms of the binomials, we need factors of -1. This would have to be 1 and -1.

Also, we need to make sure that we get the right combination of these factors.

Possible Factors

Check using the FOIL method
Tutorial 26 (Multiplying Polynomials)

First try:

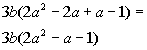
This is our original polynomial.
So this is the correct combination of factors for this polynomial.

(return to problem 1b)

Answer/Discussion to 1c

Note that this trinomial does not have a GCF.

Step 1: Substitute x for the non-coefficient part of the middle term.

Since x is already being used in this problem, let's use y for our substitution.

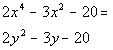
Let	*Substitute y in for x squared

Step 2: If the trinomial is in the form OR

, factor it accordingly.

Now it is in a form that we do know how to factor.

In the first terms of the binomials we need factors of 2 y squared. This would have to be 2y and y.

In the second terms of the binomials we need factors of -20. This would have to be -5 and 4, 5 and -4, -2 and 10, 2 and -10, 20 and -1, or -20 and 1 .

Also we need to make sure that we get the right combination of these factors.

Possible Factors

Check using the FOIL method
Tutorial 26: Multiplying Polynomials

First try:

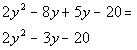
This is our original polynomial.
So this is the correct combination of factors for this polynomial.

Step 3: Substitute back in what you replaced x with in step 1.

*Substitute x squared back in for y

Note that if we would multiply this out, we would get the original trinomial.

(return to problem 1c)

Answer/Discussion to 1d

Note that this trinomial does not have a GCF.

Step 1: Set up a product of two ( ) where each will hold two terms.

It will look like this: ( )( )

Step 2: Find the factors that go in the first positions.

Since we have x squared as our first term, we will need the following:

(x )(x )

Step 3: Find the factors that go in the last positions.

We need two numbers whose product is 10 and sum is -4.

Can you think of any????

Since the product is a positive number and the sum is a negative number, we only need to consider pairs of numbers where both signs are negative.

One pair of factors of 10 is -10 and -1, which does not add up to be -4.
Another pair of factors are -2 and -5, which also does not add up to -4.

Since we have looked at ALL the possible factors, and none of them worked, we can say that this polynomial is prime. In other words, it does not factor.

(return to problem 1d)

(Back to the tutorial on factoring trinomials)