b b 2 c b g c Title
West Texas A&M University - Home
Virtual Math Lab

Intermediate Algebra
Tutorial 24: Exponents and Scientific Notation, Part II
WTAMU > Virtual Math Lab > Intermediate Algebra  



deskLearning Objectives

 
After completing this tutorial, you should be able to:
  1. Simplify exponential expressions involving raising a base to two exponents, raising a product to an exponent and raising a quotient to an exponent. 
  2. Multiply and divide numbers written in scientific notation.




desk Introduction


This tutorial picks up where Tutorial 23: Exponents and Scientific Notation Part I left off.  It finishes the rules of exponents with raising a base to two exponents, raising a product to an exponent and raising a quotient to an exponent.  Also we will revisit the concept of scientific notation.  Like it or not, the best way to master these exponents is to work through exponent problems.  So I guess we better get to it.

 

 

desk Tutorial

 
 

Base Raised to Two Exponents
Specific Illustration

 
 
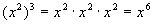
Let’s first start by using the definition of exponents as well as the law for multiplying like bases (both found in Tutorial 23: Exponents and Scientific Notation Part I, to help you to understand how we get to the law for raising a base to two exponents:

two exponents

Note how 2 times 3 is 6, which is the exponent of the final answer.   We can think of this as 3 groups of 2, which of course would come out to be 6.


 

Base Raised to two Exponents
in general,

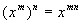
two exponents

 
In other words, when you raise a base to two exponents, you multiply those exponents together.

Again, you can think of it as n groups of m if it helps you to remember.
 

notebook Example 1:   Simplify example 1a.

 
example 1b
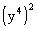*When raising a base to 2 powers you mult. your exponents

 
 
 
A Product Raised to an Exponent
Specific Illustration

 
Let’s first start by using the definition of exponents, found in Tutorial 23: Exponents and Scientific Notation Part I, to help you to understand how we get to the law for raising a product to an exponent:

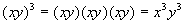
product of bases

Note how both bases of your product ended up being raised by the exponent of 3.


 

A Product Raised to an Exponent
in general,

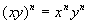
product of bases

 
In other words, when you have a PRODUCT (not a sum or difference) raised to an exponent, you can simplify by raising each base in the product to that exponent.
 

notebook Example 2:   Simplify example 2a.

 
example 2b
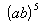*When raising a product to an exponent, raise each base of the product to that exponent

 
 
 
 
A Quotient Raised to an Exponent
Specific Illustration

 
Let’s first start by using the definition of exponents, found in Tutorial 23: Exponents and Scientific Notation Part I, to help you to understand how we get to the law for raising a quotient to an exponent:

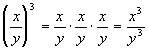
quotient rule

Since, division is really multiplication of the reciprocal, it has the same basic idea as when we raised a product to an exponent.


 

A Quotient Raised to an Exponent
in general,

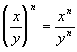
quotient rule

 
 
In other words, when you have a QUOTIENT (not a sum or difference) raised to an exponent, you can simplify by raising each base in the numerator and denominator of the quotient to that exponent.
 

notebook Example 3:   Simplify example 3a.

 
example 3b
 

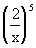*When raising a quotient to an exponent, raise each base of the quotient to that exponent

*Use def. of exponents to evaluate

 
 
Of course, we all know that life isn’t so cut and dry.  A lot of times you are needing to use more than one definition or law of exponents to get the job done.  What we did above and in Tutorial 23: Exponents and Scientific Notation Part I was to set the foundation to make sure you have a good understanding of the different ideas associated with exponents.  Next we will work through some problems which will intermix these different laws.

 
 
notebook Example 4:   Simplify.  Use positive exponents to write the answer.
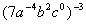example 4a

 
example 4b

*Rewrite with a pos. exp. by taking recip. of base
 
 

 

 
 
 
notebook Example 5:   Simplify.  Use positive exponents to write the answer.
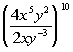example 5a

 
example 5b

*Raise each base to 10
*Mult. your exponents

 

 
 
 
notebook Example 6:   Simplify.  Use positive exponents to write the answer.
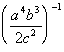example 6a

 
 
example 6b

*Rewrite with a pos. exp. by taking recip. of base

 

 
 
 
notebook Example 7: Perform indicated operations. Write the result in scientific notation as shown in Tutorial 23: Exponents and Scientific Notation Part I.
example 7a

 
example 7b

 
Not quite finished.  Remember that the number has to be between 1 and 10 for it to be in scientific notation.

 
example 7c

 
 
 
notebook Example 8: Perform indicated operations. Write the result in scientific notation as shown in Tutorial 23: Exponents and Scientific Notation Part I.
example 8a

 
example 8b
 
 

*When div. like bases you sub. your exp. 
 

 

 
desk Practice Problems

  
These are practice problems to help bring you to the next level.  It will allow you to check and see if you have an understanding of these types of problems. Math works just like anything else, if you want to get good at it, then you need to practice it.  Even the best athletes and musicians had help along the way and lots of practice, practice, practice, to get good at their sport or instrument.  In fact there is no such thing as too much practice.

To get the most out of these, you should work the problem out on your own and then check your answer by clicking on the link for the answer/discussion for that  problem.  At the link you will find the answer as well as any steps that went into finding that answer.

 

pencil Practice Problems 1a - 1c: Simplify, use positive exponents to write each answer.

 


 

 

 

pencil Practice Problems 2a - 2b: Perform indicated operations,  write each result in scientific notation.

 

2b. problem 2b
(answer/discussion to 2b)

 

 


desk Need Extra Help on these Topics?


 
The following are webpages that can assist you in the topics that were covered on this page:
 

http://www.sosmath.com/algebra/logs/log3/log33/log33.html
This webpage helps with the rule for raising a base to two exponents. 

http://www.purplemath.com/modules/exponent.htm
This webpage gives an overall review of exponents.  It contains rules from both this tutorial and Tutorial 23: Exponents and Scientific Notation Part I.

http://www.ltcconline.net/greenl/courses/152A/polyExp/intexp.htm
This webpage gives an overall review of exponents.  It contains rules from both this tutorial and Tutorial 23: Exponents and Scientific Notation Part I.


 

Go to Get Help Outside the Classroom found in Tutorial 1: How to Succeed in a Math Class for some more suggestions.


 


Last revised on July 12, 2011 by Kim Seward.
All contents copyright (C) 2001 - 2011, WTAMU and Kim Seward. All rights reserved.