

![]() Answer:
Answer:
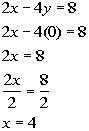
y-intercept
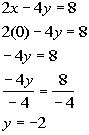
Find another solution by letting x = 1
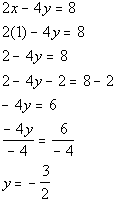
Solutions:
x
y
(x, y)
4
0
(4, 0)
0
-2
(0, -2)
1
-3/2
(1, -3/2)
Plotting the ordered pair solutions and drawing the line:
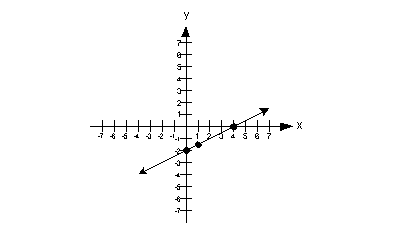
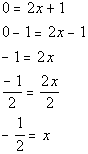
y-intercept
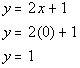
Find another solution by letting x = 1.
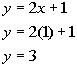
Solutions:
x
y
(x, y)
-1/2
0
(-1/2, 0)
0
1
(0, 1)
1
3
(1, 3)
Plotting the ordered pair solutions and drawing the line:
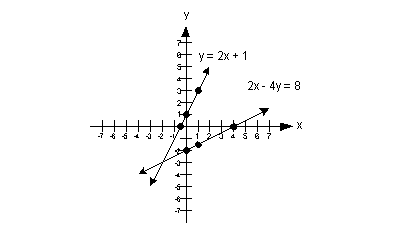
The answer is yes, they intersect at (-2, -3).
The solution to this system is (-2, -3).
![]() Answer:
Answer:
Second equation solved for y:
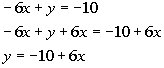
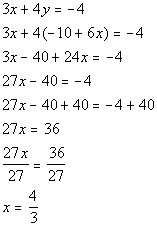
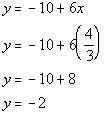
(4/3, -2) is a solution to our system.
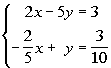
![]() Answer:
Answer:
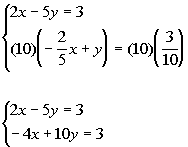
Multiplying the first equation by 2 we get:
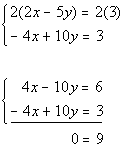
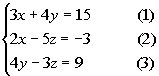
![]() Answer:
Answer:
Since z is already eliminated from the
first equation we will use that first equation in it's original form for
this step:
Multiplying the third equation by -1 and adding this to the first
equation we get:
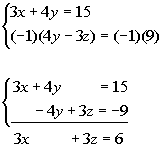
Multiplying equation (2) by 3 and equation (4) by -2 and then adding
them together we get:
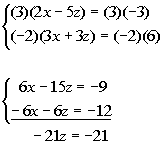
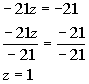
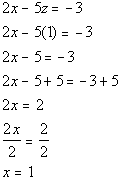
I choose equation (1) to plug in 1 for x that we found:
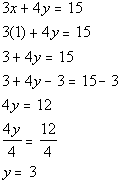
(1, 3, 1) is a solution to our system.
![]() Answer:
Answer:
Since we are looking for two different rates, we will let
x = rate of the boat
y = the rate of the current
Keep in mind that the current is affecting the overall speed.
When the boat is going downstream, it will be going faster. That rate will be x + y.
When the boat is going upstream, it will be going slower. That
rate will be x - y.
(Rate)
(Time)
= Distance
Downstream
x + y
2
20
Upstream
x - y
6
12
Equation (1):
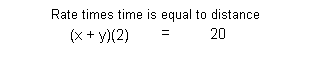
Equation (2):
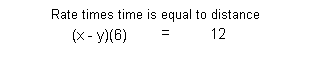
![]()
We can simplify this by dividing both sides of equation (1) by 2
and equation (2) by 6 getting rid of the ( ):
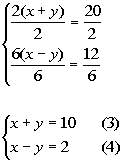
Since we already have opposite coefficients
on y, we can go right into adding equations (3) and (4) together:
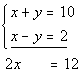
Solving for x we get:
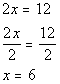
Using equation (3) to plug in 6 for x and solving for y we get:
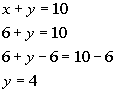
Final Answer:
The boat speed is 6 mph and the current speed is 4 mph.
![]() Answer:
Answer:
Since we are looking for three numbers, we will let
x = the smallest number
y = middle number
z = the largest number
Equation (1):
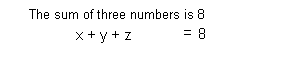
Equation (2):
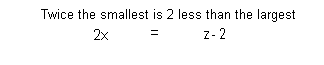
Equation (3):
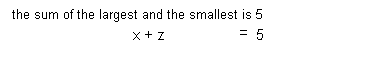
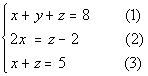
Equation (2) needs to be put in the correct form:
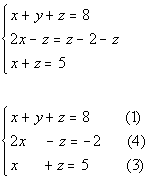
Since y is already eliminated in equation (4) and (3), it would be quickest and easiest to eliminate y.
We can use equation (4) as one equation with y eliminated:
We can use equation (3) as another equation with y eliminated:
Putting those two equations together we get:
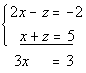
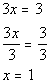
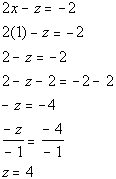
Using equation (1) to plug 1 in for x and 4 for z and solving for y we get:
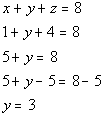
Final Answer:
1 is the smallest number, 3 is the middle number and 4 is the largest
number.
Last revised on July 6, 2011 by Kim Seward.
All contents copyright (C) 2001 - 2011, WTAMU and Kim Seward.
All rights reserved.