Intermediate Algebra
Answer/Discussion to Practice Problems
Tutorial 15: The Slope of a Line
 Answer/Discussion
to 1a Answer/Discussion
to 1a
(3, 5) and (-1, -8) |
|
*Plug in x and y values into slope formula
*Simplify
|
 Answer/Discussion
to 1b Answer/Discussion
to 1b
(4, 2) and (4, -2) |
|
*Plug in x and y values into slope formula
*Simplify
|
 Answer/Discussion
to 2a Answer/Discussion
to 2a
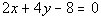
First, we need to write it in the slope/intercept form: |
|
*Sub. 2x from
both sides
*Inverse of mult. by 4 is div. by 4
*Written in slope/intercept form
|
Lining up the form with the equation we got, can you see what the slope
and y-intercept are?
It looks like our slope is -1/2 and our y-intercept
is 2.
(return to
problem 2a) |
 Answer/Discussion
to 2b Answer/Discussion
to 2b
x = -2
Note how we do not have a y. This
type of linear equation was shown in Tutorial
14 (Graphing Linear Equations). When we have x = c, where c is
a constant, then this graph is what type of line?
If you said vertical, you are correct.
Since this is a special type of linear equation that can't be written
in the slope/intercept form, I'm going to give you a visual of what is
happening and then from that let's see if we can't figure out the slope
and y-intercept.
The graph would look like this:
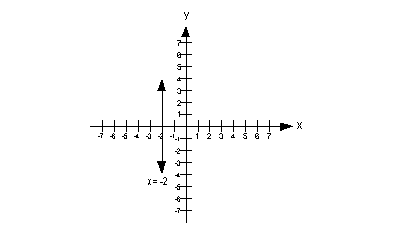
|
First, let's talk about the slope. Note that all the x values
on this graph are -2. That means the change in x,
which is the denominator of the slope formula, would be -2 - (-2) = 0.
Well you know that having a 0 in the denominator is a big no no.
This means the slope is undefined. As shown above, whenever you
have a vertical line your slope is undefined.
Now, let's look at the y-intercept.
Looking at the graph, you can see that this graph never crosses the y-axis,
therefore there is no y-intercept either.
Another way to look at this is the x value
has to be 0 when looking for the y-intercept
and in this problem x is always -2.
Final answer, the slope is undefined and the y-intercept
does not exist.
(return to
problem 2b) |
 Answer/Discussion
to 2c Answer/Discussion
to 2c
y = -1
Note how we do not have an x. This
type of linear equation was shown in Tutorial
14 (Graphing Linear Equations). When we have y = c, where c is a constant, then this graph is what type of line?
If you said horizontal, you are correct.
Since this is a special type of linear equation that can't be written
in the slope/intercept form, I'm going to give you a visual of what is
happening and then from that let's see if we can't figure out the slope
and y-intercept.
The graph would look like this:
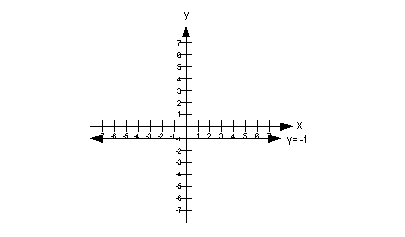
|
First, let's talk about the slope. Note how all of the y values on this graph are -1. That means the change in y,
which is the numerator of the slope formula would be -1 - (-1) = 0. Having
0 in the numerator and a non-zero number in the denominator means only
one thing. The slope equals 0.
Now, let's look at the y-intercept.
Looking at the graph, you can see that this graph crosses the y-axis
at (0, -1). So the y-intercept is (0, -1).
The slope is 0 and the y-intercept is
-1.
(return to
problem 2c) |
 Answer/Discussion
to 3a Answer/Discussion
to 3a
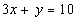 and and 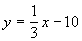
Rewriting the first equation in slope/intercept form we get: |
The slope of that first equation is -3 and the slope of the
2nd equation is 1/3.
It appears that these slopes are negative reciprocals of each other,
so that means the lines would have to be perpendicular to each other.
(return to problem
3a) |
 Answer/Discussion
to 3b Answer/Discussion
to 3b
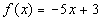 and
and 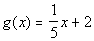
The equations are already in the slope/intercept form, so let's go right
to looking for the slope. What did you find?
I found that the slope of the first equation is -5 and the slope
of the second equation is 1/5. So what does that mean?
Well, since the two slopes are negative reciprocals of each other, the lines have to be perpendicular.
(return to problem
3b) |

Last revised on July 3, 2011 by Kim Seward.
All contents copyright (C) 2001 - 2011, WTAMU and Kim Seward.
All rights reserved.
|
|


