College Algebra
Tutorial 57: Combinations
 Learning Objectives
After completing this tutorial, you should be able to:
- Use combinations to solve a counting problem involving groups.
|
Introduction
In this tutorial we will be going over combinations. When you
need to count the number of groupings, without regard to order, then combinations
are the way to go. Recall that permutations specifically count the
number of ways a task can be arranged or ordered. That is the difference
between the two, permutations is with regard to order and combinations
is without regard to order. If you need a review on permutations,
feel free to go to Tutorial 56: Permutations.
Let's see what you can do with these combinations. |
Tutorial
|
Combination
An arrangement of r objects,
WITHOUT regard to ORDER and without repetition,
selected from n distinct objects is called
a
combination of n objects taken r at
a time.
The number of such combinations is denoted by
|
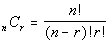
The difference between combinations and permutations is in combinations
you are counting groups (order is not important) and in permutations you
are counting different ways to arrange items with regard to order.
The n and the r mean the same thing in both the permutation and combinations, but the formula
differs. Note that the combination has an extra r!
in its denominator.
If you need review on permutations or factorials, feel free to go to Tutorial
56: Permutations. |
 Example
1: In a conference of 9 schools, how many intraconference
football games are played during the season if the teams all play each
other exactly once? |
When the teams play each other, order does not matter, we are
counting match ups. For each game there is a group of two teams playing.
So we can use combinations to help us out here.
Note that if we were putting these teams in any kind of order, then
we would need to use permutations to solve the problem.
But in this case, order does not matter, so we are going to use combinations.
First we need to find n and r :
If n is the number of teams we have to
choose from, what do you think n is in
this problem?
If you said n = 9 you are correct!!!
There are 9 teams in the conference.
If r is the number of teams we are using
at a time, what do you think r is?
If you said r = 2, pat yourself on
the back!! 2 teams play per game. |
Let's put those values into the combination formula and see what
we get: |
|
*n = 9, r = 2
*Eval. inside ( )
*Expand 9! until it gets to 7!
which is the larger ! in the den.
*Cancel out 7!'s
|
If you have a factorial key, you can put it in as 9!, divided by
7!, divided by 2! and then press enter or =.
If you don't have a factorial key, you can simplify it as shown above
and then enter it in. It is probably best to simplify it first, because
in some cases the numbers can get rather large, and it would be cumbersome
to multiply all those numbers one by one.
Wow, this means there are 36 different games in the conference. |
Example
2: You are going to draw 4 cards from a standard
deck of 52 cards. How many different 4 card hands are possible? |
This would be a combination problem, because a hand would be
a group of cards without regard to order.
Note that if we were putting these cards in any kind of order, then
we would need to use permutations to solve the problem.
But in this case, order does not matter, so we are going to use combinations.
First we need to find n and r :
If n is the number of cards we have to
choose from, what do you think n is in
this problem?
If you said n = 52 you are correct!!!
There are 52 cards in a deck of cards.
If r is the number of cards we are using
at a time, what do you think r is?
If you said r = 4, pat yourself on
the back!! We want 4 card hands. |
Let's put those values into the combination formula and see what
we get: |
|
*n = 52, r = 4
*Eval. inside ( )
*Expand 52! until it gets to 48!
which is the larger ! in the den.
*Cancel out 48!'s
|
If you have a factorial key, you can put it in as 52!, divided by
48!, divided by 4! and then press enter or =.
If you don't have a factorial key, you can simplify it as shown above
and then enter it in. It is probably best to simplify it first, because
in some cases the numbers can get rather large, and it would be cumbersome
to multiply all those numbers one by one.
Wow, this means there are 270,725 different 4 card hands. |
Example
3: 3 marbles are drawn at random from a bag containing
3 red and 5 white marbles. Answer the following questions (a - d): |
3a. How many different draws are there? |
This would be a combination problem, because a draw would be
a group of marbles without regard to order. It is like grabbing
a handful of marbles and looking at them.
Note that there are no special conditions placed on the marbles that
we draw, so this is a straight forward combination problem.
Note that if we were putting these marbles in any kind of order, then
we would need to use permutations to solve the problem.
But in this case, order does not matter, so we are going to use combinations.
First we need to find n and r:
If n is the number of marbles we have to
choose from, what do you think n is in
this problem?
If you said n = 8 you are correct!!!
There are 3 red and 5 white marbles for a total of 8 marbles.
If r is the number of marbles we are drawing
at a time, what do you think r is?
If you said r = 3, pat yourself on
the back!! 3 marbles are drawn at a time. |
Let's put those values into the combination formula and see what
we get: |
|
*n = 8, r = 3
*Eval. inside ( )
*Expand 8! until it gets to 5!
which is the larger ! in the den.
*Cancel out 5!'s
|
If you have a factorial key, you can put it in as 8!, divided by
5!, divided by 3! and then press enter or =.
If you don't have a factorial key, you can simplify it as shown above
and then enter it in. It is probably best to simplify it first, because
in some cases the numbers can get rather large, and it would be cumbersome
to multiply all those numbers one by one.
Wow, this means there are 56 different draws. |
3b. How many different draws would contain only red marbles? |
| This would be a combination problem, because a draw would be
a group of marbles without regard to order. It is like grabbing
a handful of marbles and looking at them.
In part a above,
we looked at all possible draws. From that list we only want the
ones that contain only red.
Let's see what the draw looks like: we would have to have 3
red marbles to meet this condition:
3 RED
First we need to find n and r :
If n is the number of RED marbles
we have to choose from, what do you think n is in this problem?
If you said n = 3 you are correct!!!
There are a total of 3 red marbles.
If r is the number of RED marbles
we are drawing at a time, what do you think r is?
If you said r = 3, pat yourself on
the back!! 3 RED marbles are drawn at a time. |
Let's put those values into the combination formula and see what
we get: |
|
*n = 3, r = 3
*Eval. inside ( )
*Cancel out 3!'s
|
If you have a factorial key, you can put it in as 3!, divided by
0!, divided by 3! and then press enter or =.
If you don't have a factorial key, you can simplify it as shown above
and then enter it in. It is probably best to simplify it first, because
in some cases the numbers can get rather large, and it would be cumbersome
to multiply all those numbers one by one.
This means there is only 1 draw out of the 56 found in part a that would contain 3 RED marbles. |
3c. How many different draws would contain 1 red and 2 white
marbles? |
This would be a combination problem, because a draw would be
a group of marbles without regard to order. It is like grabbing
a handful of marbles and looking at them.
In part a above,
we looked at all possible draws. From that list we only want the
ones that contain 1 RED and 2 WHITE marbles.
Let's see what the draw looks like: we would have to have 1
red and 2 white marbles to meet this condition:
1 RED 2 WHITE
First we need to find n and r:
Together that would make up 1 draw. We are going to have to use
the counting principle to help us with this one. If you need a review
on the Fundamental Counting Principle, feel free to got to Tutorial
55: The Fundamental Counting Principle.
Note how 1 draw is split into two parts - red and white. We can
not combine them together because we need a particular number of each one. So
we will figure out how many ways to get 1 RED and how many ways to get
2 WHITE, and using the counting principle, we will multiply these numbers
together.
1 RED:
If n is the number of RED marbles
we have to choose from, what do you think n is in this problem?
If you said n = 3 you are correct!!!
There are a total of 3 RED marbles.
If r is the number of RED marbles
we are drawing at a time, what do you think r is?
If you said r = 1, pat yourself on
the back!! 1 RED marble is drawn at a time.
|
2 WHITE:
If n is the number of WHITE marbles
we have to choose from, what do you think n is in this problem?
If you said n = 5 you are correct!!!
There are a total of 5 WHITE marbles.
If r is the number of WHITE marbles
we are drawing at a time, what do you think r is?
If you said r = 2, pat yourself on
the back!! 2 WHITE marbles are drawn at a time. |
|
Let's put those values into the combination formula and see what
we get: |
 |
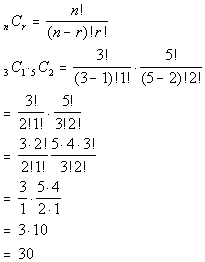*RED: n = 3, r = 3
*WHITE: n = 5, r = 2
*Eval. inside ( )
*Expand 3! until it gets to 2!
*Expand 5! until it gets to 3!
*Cancel out 2!'s and 3!'s
|
If you have a factorial key, you can put it in as 3!, times 5!,
divided by 2!, divided by 1!, divided by 3!, divided by 2! and then press
enter or =.
If you don't have a factorial key, you can simplify it as shown above
and then enter it in. It is probably best to simplify it first, because
in some cases the numbers can get rather large, and it would be cumbersome
to multiply all those numbers one by one.
This means there are 30 draws that would contain 1 RED and 2 WHITE
marbles. |
3d. How many different draws would contain exactly 2 red marbles? |
This would be a combination problem, because a draw would be
a group of marbles without regard to order. It is like grabbing
a handful of marbles and looking at them.
In part a above,
we looked at all possible draws. From that list we only want the
ones that contain 2 RED and 1 WHITE marbles. Remember that we need
a total of 3 marbles in the draw. Since we have to have 2 red, that
leaves us needing 1 white to complete the draw of 3.
Let's see what the draw looks like: we would have to have 2
red and 1 white marbles to meet this condition:
2 RED 1 WHITE
First we need to find n and r:
Together that would make up 1 draw. We are going to have to use
the counting principle to help us with this one. If you need a review
on the Fundamental Counting Principle, feel free to got to Tutorial
55: The Fundamental Counting Principle.
Note how 1 draw is split into two parts - red and white. We can
not combine them together because we need a particular number of each one. So
we will figure out how many ways to get 2 RED and how many ways to get
1 WHITE, and using the counting principle, we will multiply these numbers
together.
2 RED:
If n is the number of RED marbles
we have to choose from, what do you think n is in this problem?
If you said n = 3 you are correct!!!
There are a total of 3 RED marbles.
If r is the number of RED marbles
we are drawing at a time, what do you think r is?
If you said r = 2, pat yourself on
the back!! 2 RED marble is drawn at a time.
|
1 WHITE:
If n is the number of WHITE marbles
we have to choose from, what do you think n is
in this problem?
If you said n = 5 you are correct!!!
There are a total of 5 WHITE marbles.
If r is the number of WHITE marbles
we are drawing at a time, what do you think r is?
If you said r = 1, pat yourself on
the back!! 1 WHITE marble are drawn at a time. |
|
Let's put those values into the combination formula and see what
we get: |
 |
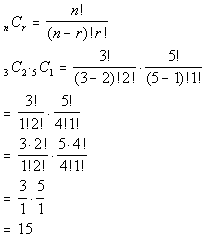*RED: n = 3, r = 2
*WHITE: n = 5, r = 1
*Eval. inside ( )
*Expand 3! until it gets to 2!
*Expand 5! until it gets to 4!
|
If you have a factorial key, you can put it in as 3!, times 5!,
divided by 1!, divided by 2!, divided by 4!, divided by 1! and then press
enter or =.
If you don't have a factorial key, you can simplify it as shown above
and then enter it in. It is probably best to simplify it first, because
in some cases the numbers can get rather large, and it would be cumbersome
to multiply all those numbers one by one.
This means there are 15 draws that would contain 2 RED and 1 WHITE
marbles. |
Practice Problems
These are practice problems to help bring you to the next level.
It will allow you to check and see if you have an understanding of these
types of problems. Math works just like anything
else, if you want to get good at it, then you need to practice it.
Even the best athletes and musicians had help along the way and lots of
practice, practice, practice, to get good at their sport or instrument.
In fact there is no such thing as too much practice.
To get the most out of these, you should work the problem out on
your own and then check your answer by clicking on the link for the answer/discussion
for that problem. At the link you will find the answer
as well as any steps that went into finding that answer. |
 Practice Problems 1a - 1b: A teacher has 15 students and 5 are to be chosen
to give demonstrations. How many different ways can the teacher choose
the demonstrators given the following conditions.
Practice Problems 2a - 2c: A teacher has 14 freshmen, 15 sophomores, 8 juniors and 10 seniors and 8 names will be drawn from a hat to go on a trip. How many different draws of student names can the teacher have given the following conditions.
Need Extra Help on these Topics?
Last revised on May 20, 2011 by Kim Seward.
All contents copyright (C) 2002 - 2011, WTAMU and Kim Seward. All rights reserved.
|
|
