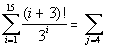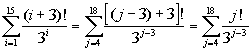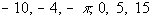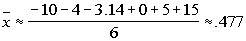College Algebra Tutorial 54
College Algebra
Answer/Discussion to Practice Problems
Tutorial 54B: Series
 Answer/Discussion
to 1a
Answer/Discussion
to 1a
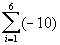
What
values will you be plugging in to get the terms that will be summed?
If you said 1 through 6 you are right on!!!
Let’s see what we get when
we add up terms plugging in 1, 2, 3, 4, 5, and 6 for i:
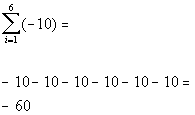
Note that the general term is -10, which is a
constant. So no matter what
i is, the term is always
-10.
Since we were going from 1 to 6, we had 6 terms of -10 be added or
6(-10) = -60.
In general, if your general term is constant than the sum will end up
being the number of terms in your series times the constant.
 Answer/Discussion
to 1b
Answer/Discussion
to 1b
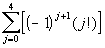
What values will you
be plugging in to get the terms that will be summed?
If you said 0 through 4
you are right on!!!
Let’s see what we get
when we add up terms plugging in 0, 1, 2, 3, and 4, for j:
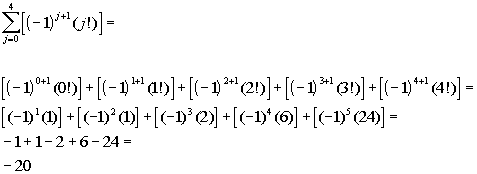
If you need a review on
factorials, feel free to go to Tutorial 54A: Sequences.
 Answer/Discussion
to 2a
Answer/Discussion
to 2a
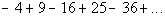
There are two things that change.
First
let's look at the alternating signs:
The first term is
negative, the second term is positive, the third negative, the fourth
positive and so forth.
When
i is odd (1,
3, 5, ...), then the term is negative.
When
i is even (2,
4, 6, ...), then the term is positive.
So do you think we are going to have
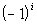
or
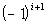
.
If you said
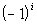
you are
correct!!! If
n is odd, then this term will be negative. If
n is even, then this term
will be positive.
Next, let’s look at the number on each term.
We need to figure out the relationship between i and the exponent:
We
need to figure out the relationship between i and the number:
When i is 1, the number is 4
When i is 2, the
number is 9.
When i is 3, the
number is 16.
When i is 4, the number is 25.
When i is 5, the
number is 36.
And so forth....
What
do you think the relationship is?
It looks like we have a series of perfect squares. However, since
we have to start with
i = 1, we will have to adjust it so that the first term has a 4 in
it.
So
how will we represent the number?
If you said
i + 1,
give yourself a pat on the back.
Putting it together, we can write the summation as
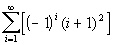
.
Sometimes you have to play around with it before you get it just
right. You can always check it by putting in the
i values and seeing if you
get the given series.
This one does check.
 Answer/Discussion
to 3a
Answer/Discussion
to 3a
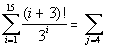
We need to rewrite the series so that they are both
equivalent to each other, but the first one starts at
i = 1 and the second one
starts at
j = 4.
We
need to find the relationship between n and j and rewrite n in terms of j:
Looking at the lower limits for each, how would you write
n in terms of
j? What is their
relationship?
If you said
i =
j - 3, you are
correct!!!
Basically, we need to do a substitution. Wherever we have an
n in our general term, we
will replace it with
j - 3:
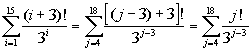
 Answer/Discussion
to 4a
Answer/Discussion
to 4a
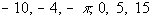
Note that I will be rounding to 3.14.
We
need to find the mean, so we will be adding all of the values that we
have and dividing that sum by what number?
If you said 6, you are correct!
Let’s see what we get:
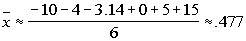

Last revised on May 16, 2011 by Kim Seward.
All contents copyright (C) 2002 - 2011, WTAMU and Kim Seward. All rights reserved.


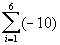
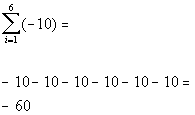
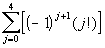
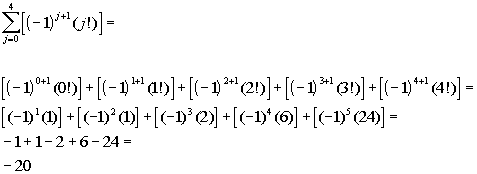
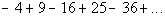
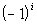 or
or 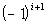 .
.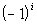 you are
correct!!! If n is odd, then this term will be negative. If n is even, then this term
will be positive.
you are
correct!!! If n is odd, then this term will be negative. If n is even, then this term
will be positive.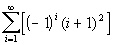 .
.