

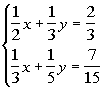
Multiplying each equation by it's respective LCD we get:
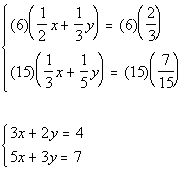
*Mult. by LCD of 15
Note how the coefficient on y in the first equation is 2 and in the second equation it is 3. We need to have opposites, so if one of them is 6 and the other is -6, they would cancel each other out when we go to add them. If we added them together the way they are now, we would end up with one equation and two variables, nothing would drop out. And we would not be able to solve it.
So I proposed that we multiply the first equation by
3 and the second
equation by -2, this would create a 10 and a -10 in front of the y’s
and we will have our opposites.
Multiplying the first equation by 3 and the second equation by -2 we get:
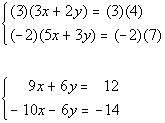
*y's
have opposite
coefficients
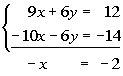
I choose to plug in 2 for x into the first simplified equation (found in step 1) to find y’s value.
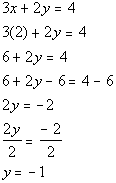
*Inverse of add 6 is sub. 6
*Inverse of mult. by 2 is div.
by 2
(2, -1) is a solution to our system.
![]()
It does not matter which equation or which variable you choose to solve for. But it is to your advantage to keep it as simple as possible.
First equation solved for y:
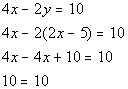
*Variable dropped out AND true
As mentioned above, if the variable drops out AND we have a TRUE statement, then when have an infinite number of solutions. They end up being the same line.
When they end up being the same equation, you have an infinite number of solutions. You can write up your answer by writing out either equation to indicate that they are the same equation.
Two ways to write the answer are {(x, y)| y = 2x - 5} OR {(x, y) | 4x - 2y = 10}.
![]()
Note how the coefficient on x in the first equation is 2 and in the second equation it is -4. We need to have opposites, so if one of them is 4 and the other is -4, they would cancel each other out when we go to add them. If we added them together the way they are now, we would end up with one equation and two variables, nothing would drop out. And we would not be able to solve it.
So I proposed that we multiply the first equation by
2, this
would create a 4 and a -4 in front of the x’s
and we will have our opposites.
Multiplying the first equation by 2 we get:
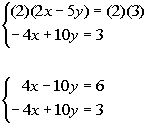
*x's
and y's
have opposite coefficients
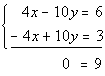
As mentioned above if your variable drops out and you have a FALSE statement, then there is no solution. If we were to graph these two, they would be parallel to each other.
The answer is no solution.
![]()
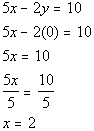
*Inverse of mult. by 5 is div. by 5
*x-intercept
y-intercept
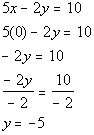
*Inverse of mult. by -2 is div. by -2
*y-intercept
Find another solution by letting x = 1.
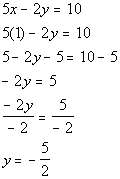
*Inverse of mult. by -2 is div.
by -2
Solutions:
Plotting the ordered pair solutions and drawing the line:
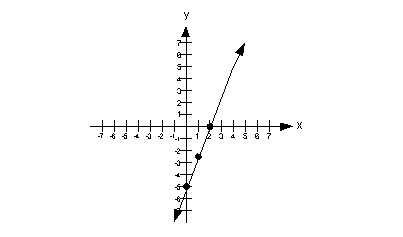
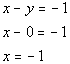
y-intercept
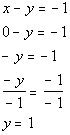
*Inverse of mult. by -1 is div. by -1
*y-intercept
Find another solution by letting x = 1.
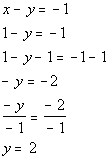
*Inverse of mult. by -1 is div by -1
Solutions:
Plotting the ordered pair solutions and drawing the line:
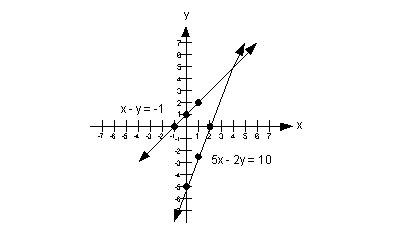
The answer is yes, they intersect at (4, 5).
The solution to this system is (4, 5).
Last revised on March 26, 2011 by Kim Seward.
All contents copyright (C) 2002 - 2011, WTAMU and Kim Seward. All rights reserved.