

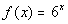
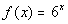 (x, y)
-2
(x, y)
-2
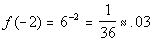
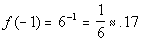
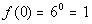
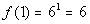
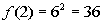
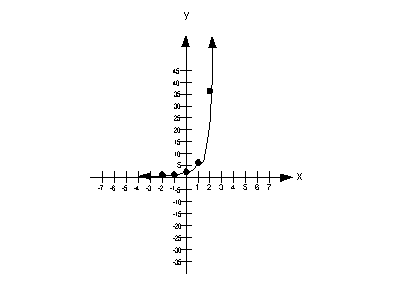
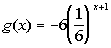
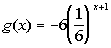 (x, y)
-2
(x, y)
-2
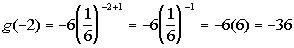
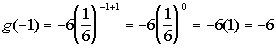
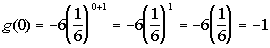
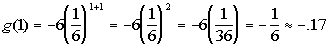
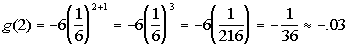
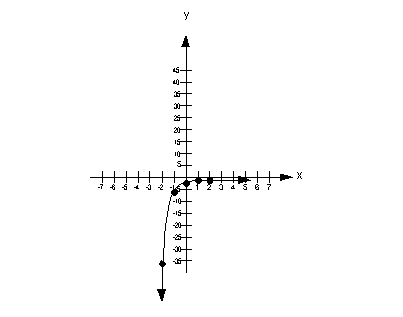
P = 25000
r = 3.25% = .0325
t = 21
n = quarterly = 4 times
a year
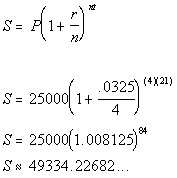
Compound Amount: $49334.23
Compound Interest: $24334.23
P = 4525
r = 9.5% = .095
t = 12
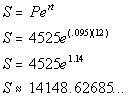
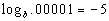

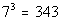
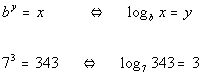
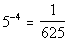
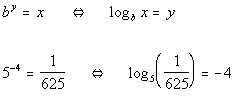
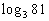
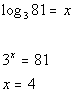
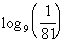
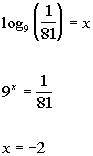
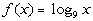
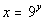
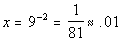
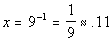
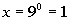
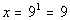
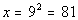
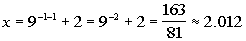
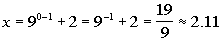
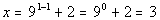
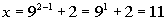
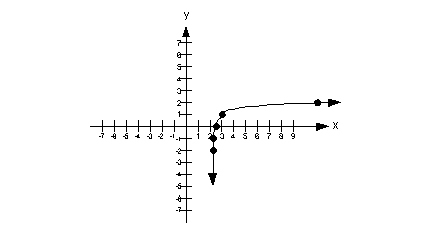
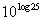
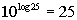
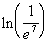
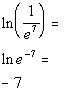
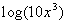
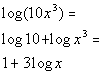
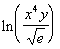
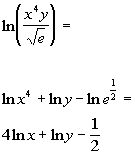
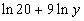
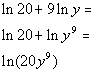
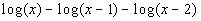
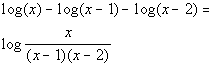
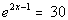
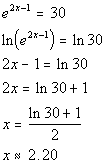
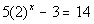
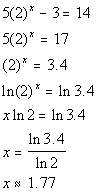
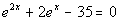
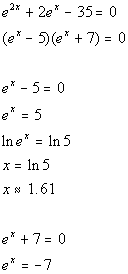
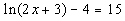
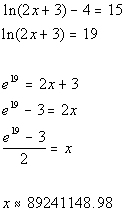
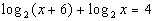
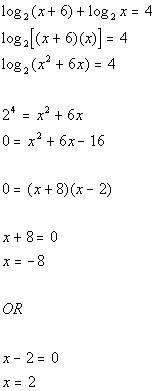
Last revised on March 25, 2011 by Kim Seward.
All contents copyright (C) 2002 - 2011, WTAMU and Kim Seward.
All rights reserved.