College Algebra Tutorial 41

---

 

 

VERTEX

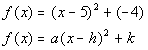
Since (h, k) is the vertex in standard form then the vertex is  (5, -4).
 

MAX OR MIN?
Since a = 1, and 1 is greater than 0, this parabola would open up.

So our vertex (5, -4) is the minimum point.

 

 

VERTEX

Using the vertex formula we get:

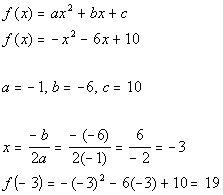
The vertex would be (-3, 19)
 

MAX OR MIN?
Since a = -1, and -1 is less than 0, this parabola would open down.

So our vertex (-3, 19) is a maximum point.

 

 

 

CURVE
Since a = -1 and -1 < 0, then it looks like it is going to curve down. 

VERTEX

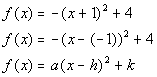
Vertex is (-1, 4)
 

INTERCEPTS

y-intercept:

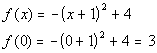
y-intercept: (0, 3)
 

x-intercept:

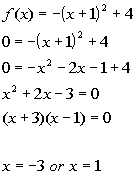
x-intercepts: (-3, 0) and (1, 0)
 

GRAPH

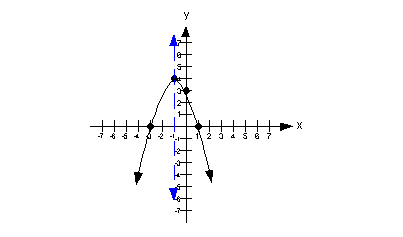
As shown on the graph, the axis of symmetry is x = -1.

 

 

CURVE
Since a = 1 and 1 > 0, then it looks like it is going to curve up. 

VERTEX

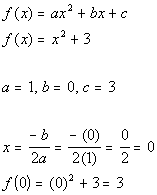
Vertex is (0, 3)
 

INTERCEPTS

y-intercept:

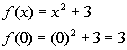
y-intercept: (0, 3)
 

x-intercept:

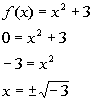
x-intercepts: 
Note how we got a negative number underneath the square root.  That means there is no real number solution.  That also means that there are NO x- intercepts.
 

GRAPH

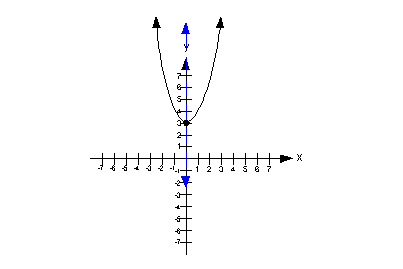
As shown on the graph, the axis of symmetry is x = 0.

 

 

 

a) LEADING COEFFICIENT TEST
Since the degree of the polynomial, 4,  is even and the leading coefficient, 1, is positive, then the graph of the given polynomial rises to the left and rises to the right.
 

b) X-INTERCEPT

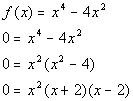
First factor:

Since the exponent on this factor is 2, then multiplicity for the zero x = 0 is 2.

Since the multiplicity is 2, which is even, then the graph touches the x-axis and turns around at the zero x = 0.
 

Second factor:

Since the exponent on this factor is 1, then multiplicity for the zero x = -2 is 1.

Since the  multiplicity is 1, which is odd, then the graph crosses the x-axis at x = -2. 
 

Third factor:

Since the exponent on this factor is 1, then multiplicity for the zero x = 2 is 1.

Since the  multiplicity is 1, which is odd, then the graph crosses the x-axis at x = 2. 
 

c) Y-INTERCEPT
Letting x = 0 we get:

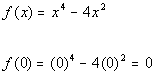
The y-intercept is (0, 0).
 

d) SYMMETRY
Y-axis symmetry:

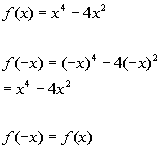
It is symmetric about the y-axis.
 

Origin symmetry:

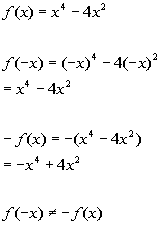
Is not symmetric about the origin.
 

e) TURNING POINTS
Since the degree of the function is 4, then there is at most 4 - 1 = 3 turning points.
 

EXTRA POINTS
To get a more accurate curve, lets find some points that are in between the points we found above:

So (-1, -3) and (1, -3) are two more points on the graph.
 

f) GRAPH

 

 

 

 

 

 

 

 

 

 

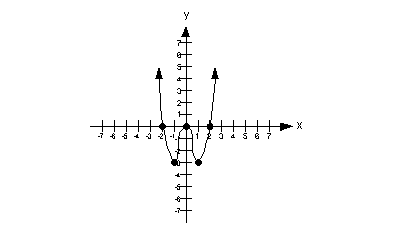
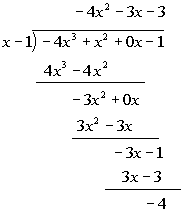
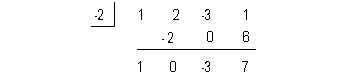
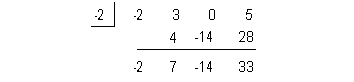
f(-2) = 33

 

 

 

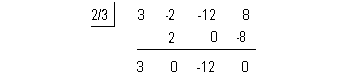
Rewriting f(x) as (x - 2/3)(quotient) we get:

 

Setting f(x) = 0 and solving we get:

 

 

 

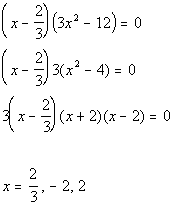
POSSIBLE ZEROS
The factors of the constant term -6 are.

The factors of the leading coefficient 1 are.

Writing the possible factors as p/q we get: 

 

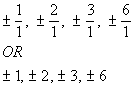
DESCARTES' RULE OF SIGNS
Possible number of positive real zeros:

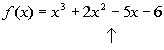
The up arrows are showing where there are sign changes between successive terms, going left to right.

There is 1 sign change between successive terms, which means there is exactly one positive real zero. 
 

Possible number of negative real zeros:

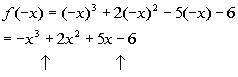
There are 2 sign changes between successive terms, which means that is the highest possible number of negative real zeros.  To find the other possible number of negative real zeros from these sign changes, you start with the number of changes, which in this case is 2, and then go down by even integers from that number until you get to 1 or 0.

Since we have 2 sign changes with f(x), then there are possibility of 2 or 2 - 2 = 0 negative real zeros.
 

FIND A ZERO
I’m going to choose -1 to try:

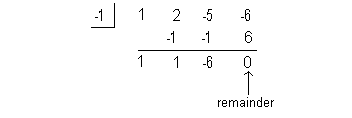
We found a number that has a remainder of 0. This means that x = -1 is a zero or root of our polynomial function.
 

FIND OTHER ZEROS
Since, x = -1 is a zero, that means x + 1 is a factor of our polynomial function.

Rewriting f(x) as (x + 1)(quotient) we get: 

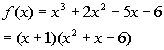
We need to finish this problem by setting this equal to zero and solving it:

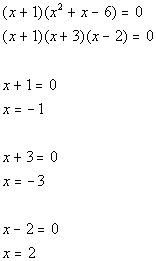
The zeros of this function are x =  -3, -1, and 2.

 

 

POSSIBLE ZEROS
The factors of the constant term -2 are.

The factors of the leading coefficient 1 are.

Writing the possible factors as p/q we get: 

 

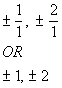
DESCARTES' RULE OF SIGNS
Possible number of positive real zeros:

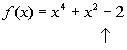
The up arrows are showing where there are sign changes between successive terms, going left to right.

There is 1 sign change between successive terms, which means there is exactly one positive real zero. 
 

Possible number of negative real zeros:

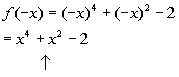
There is 1 sign change between successive terms, which means there is exactly one negative real zero.
 

FIND A ZERO
I’m going to choose 1 to try:

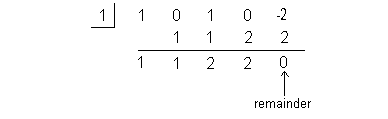
We found a number that has a remainder of 0. This means that x = 1 is a zero or root of our polynomial function.
 

FIND OTHER ZEROS
Since, x = 1 is a zero, that means x - 1 is a factor of our polynomial function.

Rewriting f(x) as (x - 1)(quotient) we get: 

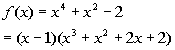
We need to finish this problem by setting this equal to zero and solving it:

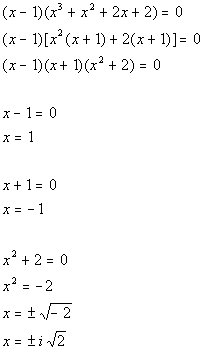
The zeros of this function are x =  -1, 1, , .

 

 

 

LOWER BOUND

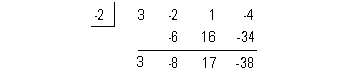
Since c = -2 < 0 AND the successive signs in the bottom row of our synthetic division alternate, then -2 is a lower bound for the real roots of this equation.
 

UPPER BOUND

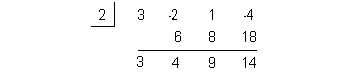
Since c = 2 > 0 AND all of the  signs in the bottom row of our synthetic division are positive, then 2 is an upper bound for the real roots of this equation.
 

Since -2 is a lower bound and 2 is an upper bound for the real roots of the equation, then that means all real roots of the equation  lie between -2 and 2.

 

 

 

Finding f(1): 

Finding f(2): 

Since there is a sign change between f(1) = -1 and f(2) = 10, then according to the Intermediate Value Theorem, there is at least one value between 1 and 2 that is a zero of this polynomial function.

Checking functional values at intervals of one-tenth for a sign change:

Finding f(1): 

Finding f(1.1): 

Finding f(1.2): 
 

Hey we have a sign change.  Now we want to find the zero to the nearest tenth.  So is it going to be x = 1.1 or x = 1.2.   We can not necessarily go by which functional value is closer to zero.  We will need to dig a little bit deeper and go by intervals of one-hundredths. 

Finding f(1.11): 

Finding f(1.12): 

Finding f(1.13): 

Finding f(1.14): 

Finding f(1.15): 

Finding f(1.16): 

Whew!!!!  At last we come to a sign change between successive hundredths.   There is a zero between 1.15 and 1.16. 

The nearest tenth would be 1.2. 

 

 

 

The complex number 2 + i is a root, that means it’s conjugate 2 - i is also a root. 

Using synthetic division with the given zero to find the quotient we get: 

 

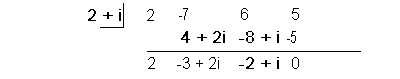
Using synthetic division with the conjugate 2 - i and the quotient found above we get:

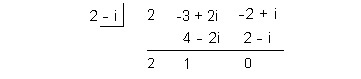
From here we can rewrite the original problem using the roots that we have above and the quotient that we ended up with in this last synthetic division.

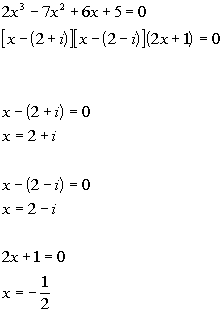
So the roots of the polynomial equation are 2 + i, 2 - i, -1/2.

 

 

 

a) FACTORS THAT ARE IRREDUCIBLE OVER RATIONAL NUMBERS

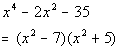
Since 7 is not a perfect square, this is as far as we can factor it using only rational numbers.
 

b) FACTORS THAT ARE IRREDUCIBLE OVER REAL NUMBERS

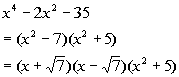
Even though 7 is not a perfect square, we can factor the first factor found above as a difference of squares and end up with an irrational number, which is still a real number.

c) COMPLETELY FACTORED OVER COMPLEX NONREAL NUMBERS

 

 

 

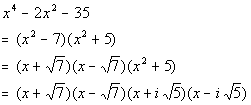
WRITE OUT ALL FACTORS OF THE POLYNOMIAL
Since our degree is 3, that means there are three linear factors over the complex numbers (possibly real and not necessarily distinct).

Note how we are only given two zeros.  We need to come up with a third one.

Since -3i is a zero, that means its conjugate, 3i, is also a zero.

Using the Linear Factorization Theorem we get:
 

MULTIPLY FACTORS

 

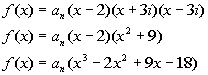
FINDING a
This problem gave another condition, f(1) = -20.

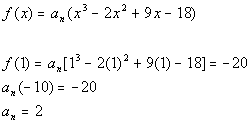
PUTTING IT ALL TOGETHER

 

 

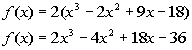
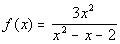
REDUCE

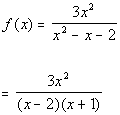
This function cannot be reduced any further.  This means that there will be no open holes on this graph.

VERTICAL ASYMPTOTES

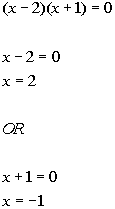
HORIZONTAL ASYMPTOTES

SYMMETRY

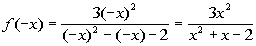
Since 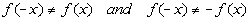, the function is neither even nor odd.  This means the graph is not symmetric about the y-axis nor the origin.

INTERCEPTS

y-intercept:

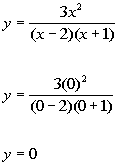
y-intercept: (0, 0)
 

x-intercept:

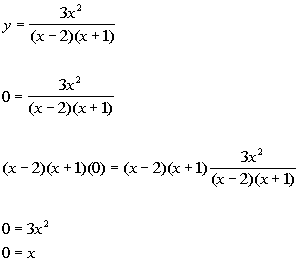
x-intercept: (0, 0)
 

GRAPH

 

---

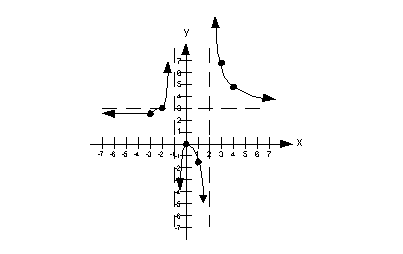
Last revised on March 20, 2011 by Kim Seward.
All contents copyright (C) 2002 - 2011, WTAMU and Kim Seward. All rights reserved.