College Algebra Tutorial 33


College Algebra
Answer/Discussion to Practice Problems  
Tutorial 33: Practice Test on Tutorials 25 - 32

WTAMU > Virtual Math Lab > College Algebra > Tutorial 33: Practice Test on Tutorials 25 - 32

 


Problems 1a - 1c:  Find the slope of the straight line that passes through the given points or state that the slope is undefined.  Then indicate if the line through the points rises (left to right), falls (left to right), is horizontal, or is vertical.

 
1a.  (7, 4) and (1, 1)
 
checkAnswer:

answer 1a

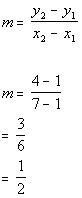
Since the slope is positive, the line would rise (left to right).

 


 

1b.  (-3, 4) and (2, -1)
 
checkAnswer:

answer 1b

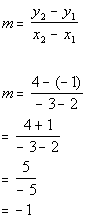
Since the slope is negative, the line would fall (left to right).

 


 

1c.  (-5, 3) and (-5, 2)
 
checkAnswer:

answer 1c

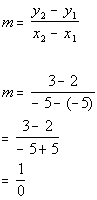
The slope is undefined.

Since the slope is undefined, the line would be vertical.

 


 
 

Problems 2a - 2d:  Write an equation for the line in point/slope form and slope/intercept form that has the given condition.

 
2a.  Slope = 3/2 and passes through the origin.
 
checkAnswer:

Point/Slope Form:
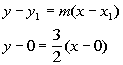
answer 2a1

Slope/Intercept Form:
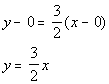answer 2a2


 

2b.   x-intercept = 4 and y-intercept = -3
 
checkAnswer:

Slope:
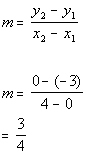
answer 2b1

Point/Slope Form:
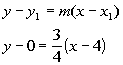
answer 2b2

Slope/Intercept Form:
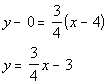
answer 2b3
 


 

2c.  Passes through (3, 2) and is parallel to 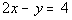problem 2c.
 
checkAnswer:

Slope:
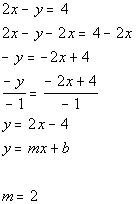
answer 2c1

Slope of line parallel to this line would be m = 2.

Point/Slope Form:
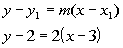
answer 2c2

Slope/Intercept Form:
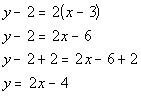answer 2c3

 


 

2d.  Passes through (-1, -1) and is perpendicular to 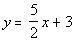problem 2d.
 
checkAnswer:
Slope:
answer 2d1

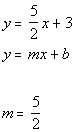
Slope of line perpendicular to this line would be m = -2/5.

Point/Slope Form:
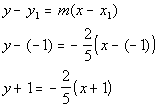
answer 2d2

Slope/Intercept Form:
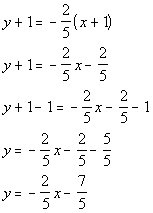answer 2d3

 


 
 

Problems 3a - 3d:  Give the slope and y-intercept of the given line and then graph it.

 
3a. 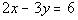problem 3a
 
checkAnswer:

Slope/Intercept Form:
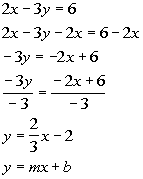
answer 3a1

Slope and y-intercept:

Lining up the equation with the slope/intercept form we get
slope = m = 2/3
y-intercept = b = -2

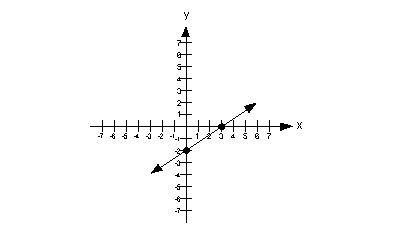
answer 3a2

 


 

3b. 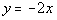problem 3b
 
checkAnswer:

Slope/Intercept Form:
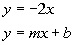
answer 3b1

Slope and y-intercept:

Lining up the equation with the slope/intercept form we get
slope = m = -2
y-intercept = b = 0

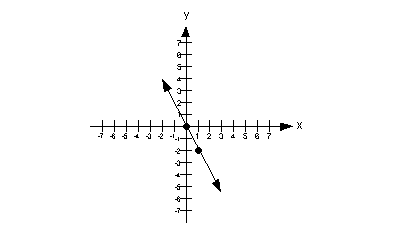
answer 3b2


 

3c. 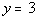problem 3c
 
checkAnswer:

Horizontal line:

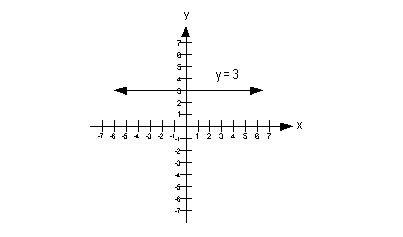
answer 3c1

Slope and y-intercept:

Slope = m = 0
y-intercept = 3


 

3d. 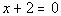problem 3d
 
checkAnswer:

answer 3d1

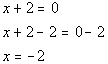
Vertical line:

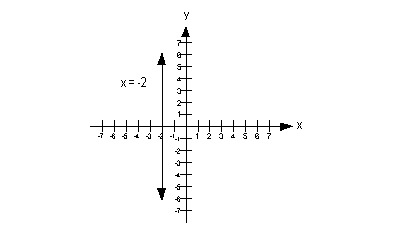
answer 3d2



Slope and y-intercept:

Slope = m = undefined
y-intercept = none


 
 

Problems 4a - 4b:  Find the slope of the line that is a) parallel and b) perpendicular to the given line.

 
4a. 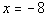problem 4a
 
checkAnswer:

Slope of the parallel line: 
Since parallel lines have the same slope and this is a vertical line, then the slope is undefined.

Slope of the perpendicular line: 
Since vertical and horizontal lines are perpendicular to each other and this is a vertical line, then the slope of the perpendicular line in this case would be the slope of a horizontal line which would be 0. 

 


 

4b. 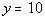problem 4b
 
checkAnswer:

Slope of the parallel line: 
Since parallel lines have the same slope and this is a horizontal line, then the slope is 0.

Slope of the perpendicular line: 
Since vertical and horizontal lines are perpendicular to each other and this is a horizontal line, then the slope of the perpendicular line in this case would be the slope of a vertical line which would be undefined. 


 
 

Problem 5a: Write the standard form of the equation of the circle with the given center and radius.

 
5a.  center (-2, 0) and r = 3
 
checkAnswer:

answer 5a


 
 

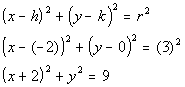
Problem 6a:  Find the center and radius of the given circle and graph it.

 
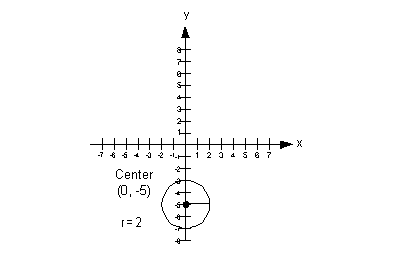
6a. 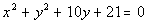problem 6a
 
 
checkAnswer:

answer 6a1

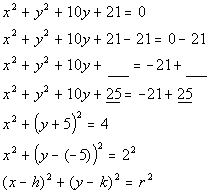
Lining up the equation with the standard form we get
center = (h, k) = (0, -5)
radius = r = 2 

answer 6a2


 


 

Problems 7a - 7b:  Determine if the given relation is function or not.  Give its domain and range. 

 
7a.  {(-1, 2), (1, 3), (-1, 4), (2, 5)}
 
 
checkAnswer:

Is this a function or not? 
Since the input value of -1 goes with two output values, 2 and 4, this relation would not be an example of a function. 
 

Domain 
The set of all input values would be {-1, 1, 2}.
 

Range 
The set of all output values would be {2, 3, 4, 5}.


 

 

7b.  {(1, 1), (2, 2), (3, 3), (4, 4)}
 
checkAnswer:

Is this a function or not? 
Since every first element (or input) corresponds with EXACTLY ONE second element (or output), this relation would be an example of a function. 
 

Domain 
The set of all input values would be {1, 2, 3, 4}.
 

Range 
The set of all output values would be {1, 2, 3, 4}.


 


 

Problems 8a - 8b:  Decide whether y is a function of x.

 
8a. 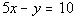problem 8a
 
checkAnswer:

answer 8a

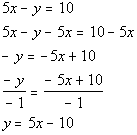
At this point we ask ourselves, would we get one value for y if you plug in any value for x? 

Since the answer to that question is yes, that means by definition, y is a function of x.

 


 

8b. 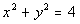problem 8b
 
checkAnswer:

answer 8b

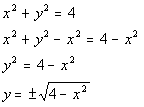
At this point we ask ourselves, would we get one value for y if you plug in any value for x? 

Since the answer to that question is no, that means by definition, y is NOT a function of x.


 


 

Problem 9a:  Find and simplify a)  f(a),  b)  f(a + h) and  c) 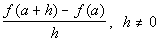problem 9a1                  using the given function.

 
9a. 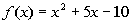problem 9a2
 
checkAnswer:

f(a):
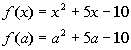
answer 9a1

f(a + h):
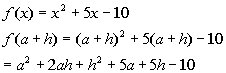
answer 9a2

Putting it all together we get:
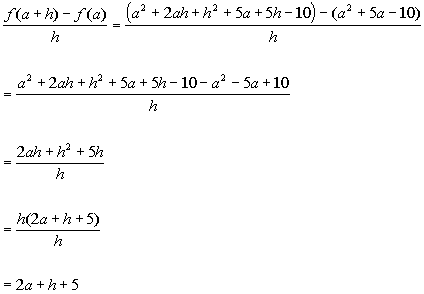answer 9a3


 


 

Problem 10a:  Find the functional values f(-5), f(1), and f(3) for the compound function.

 
10a. 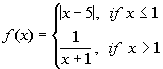problem 10a
 
checkAnswer:

To find f(-5), we need to go to the piece of the function that x = -5 would be under, which would be the first one where x < 1:

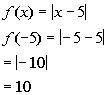
answer 10a1
 

To find f(1), we need to go to the piece of the function that x = 1 would be under, which would be the first one where x < 1:

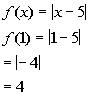
answer 10a2
 

To find f(3), we need to go to the piece of the function that x = 3 would be under, which would be the second one where x > 1.

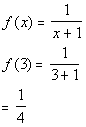
answer 10a3


 
 

 

Problems 11a - 11c:  Give the domain of the function.

 
11a. 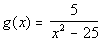problem 11a
 
checkAnswer:

answer 11a

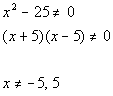
The domain would be all real numbers except -5 and 5.

 


 

11b. 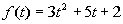problem 11b
 
checkAnswer:

The domain is all real numbers.

 


 

11c. 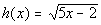problem 11c
 
checkAnswer:

answer 11c

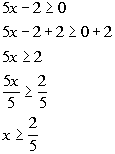
Domain is x >  2/5.


 


 

Problems 12a - 12e:  Graph the given function using the given values of x.   Also use the graph to determine the domain and range of  the function.

 
12a. problem 12a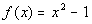; x = -3, -2, -1, 0, 1, 2, 3
 
checkAnswer:
 
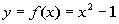
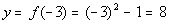
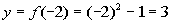
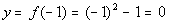
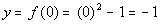
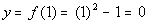
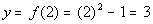
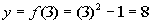
x answer 12a (x, y) -3 answer 12a2 (-3, 8) -2 answer 12a3 (-2, 3) -1 answer 12a4 (-1, 0) 0 answer 12a5 (0, -1) 1 answer 12a6 (1, 0) 2 answer 12a7 (2, 3) 3 answer 12a8 (3, 8)

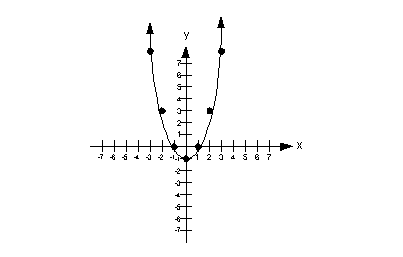
answer 12a9

Domain
Since the domain is the set all input values, it corresponds to the x-values in this problem. 

This means that the domain is 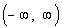answer 12a10.
 

Range
Since the range is the set all output values, it corresponds to the y-values in this problem. 

This means that the range is 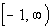answer 12a11.

 


 

12b. problem 12b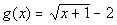; x = -1, 0, 3, 8
 
checkAnswer:
 
x answer 12b1 (x, y) -1 answer 12b2 (-1, -2) 0 answer 12b3 (0, -1) 3 answer 12b4 (3, 0) 8 answer 12b5 (8, 1)

answer 12b6

Domain
Since the domain is the set all input values, it corresponds to the x-values in this problem. 

This means that the domain is answer 12b7.
 

Range
Since the range is the set all output values, it corresponds to the y-values in this problem. 

This means that the range is answer 12b8.


 

 

12c. problem 12c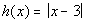; x = 0, 1, 2, 3, 4, 5, 6
 
checkAnswer:
 
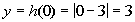
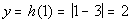
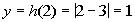
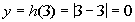
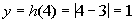
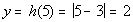
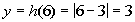
x answer 12c1 (x, y) 0 answer 12c2 (0, 3) 1 answer 12c3 (1, 2) 2 answer 12c4 (2, 1) 3 answer 12c5 (3, 0) 4 answer 12c6 (4, 1) 5 answer 12c7 (5, 2) 6 answer 12c8 (6, 3)

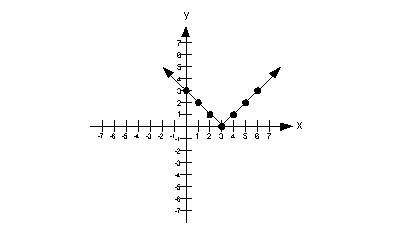
answer 12c9

Domain
Since the domain is the set all input values, it corresponds to the x-values in this problem. 

This means that the domain is 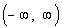answer 12a10.
 

Range
Since the range is the set all output values, it corresponds to the y-values in this problem. 

This means that the range is 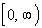answer 12c10.

 


 

12d. problem 12d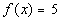; x = -3, -2, -1, 0, 1, 2, 3
 
checkAnswer:
 
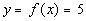
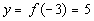
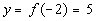
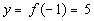
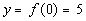
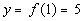
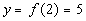
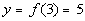
x answer 12d1 (x, y) -3 answer 12d2 (-3, 5) -2 answer 12d3 (-2, 5) -1 answer 12d4 (-1, 5) 0 answer 12d5 (0, -5) 1 answer 12d6 (1, 5) 2 answer 12d7 (2, 5) 3 answer 12d8 (3, 5)

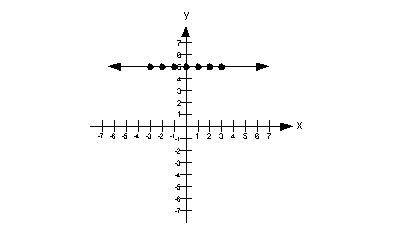
answer 12d9

Domain
Since the domain is the set all input values, it corresponds to the x-values in this problem. 

This means that the domain is 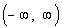answer 12a10.
 

Range
Since the range is the set all output values, it corresponds to the y-values in this problem. 

This means that the range is {y | y  = 5}.


 

 

12e. problem 12e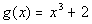; x = -2, -1, 0, 1, 2
 
checkAnswer:
 
x answer 12e1 (x, y) -2 answer 12e2 (-2, -6) -1 answer 12e3 (-1, 1) 0 answer 12e4 (0, 2) 1 answer 12e5 (1, 3) 2 answer 12e6 (2, 10)

answer 12e7

Domain
Since the domain is the set all input values, it corresponds to the x-values in this problem. 

This means that the domain is answer 12a10.
 

Range
Since the range is the set all output values, it corresponds to the y-values in this problem. 

This means that the range is answer 12a10.


 


 

Problem 13a:  Use the graph to determine a) the x-intercepts, if any b) the y-intercept, if any, c) the functional value indicated, to determine intervals on which the function is d) increasing, if any, e) decreasing, if any, and f) constant, if any.

 

13a.

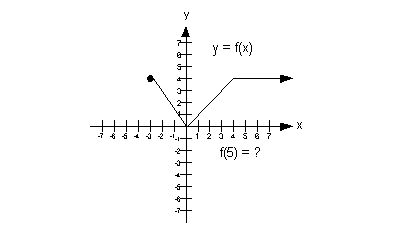
 problem 13a
 

checkAnswer:

a) x-intercept
Since the x-intercept is where the graph crosses the x-axis, the ordered pair for this x-intercept would be (0, 0).
 

b) y-intercept
Since the y-intercept is where the graph crosses the y-axis, the ordered pair for this y-intercept would be (0, 0).
 

c) Functional Value
Since the functional value correlates with the second or y value of an ordered  pair, then the functional value at x = 5 is 4. 

d) Increasing
Since a function is increasing in an interval when it is going up left to right in that interval, this function is increasing on the interval 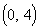answer 13a1.

e) Decreasing
Since a function is decreasing in an interval when it is going down left to right in that interval, this function is increasing on the interval 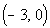answer 13a2.

f) Constant
Since a function is constant in an interval when it is horizontal in that interval, this function is constant on the interval 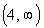answer 13a3.


 
 

Problems 14a - 14b:  Use the vertical line test to identify graphs in which y is a function of x.

 

14a.

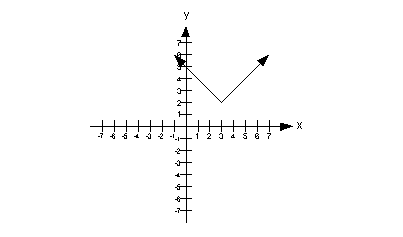
 problem 14a
 

checkAnswer:

This graph would pass the vertical line test, because there would not be any place on it that we could draw a vertical line and it would intersect it in more than one place. 

Therefore, this is a graph of a function.

 


 

14b.

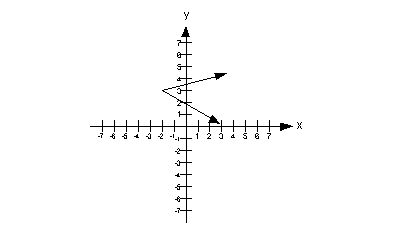
problem 14b
 

checkAnswer:

This graph would not pass the vertical line test because there is at least one place on it that we could draw a vertical line and intersect it in more than one place.

Therefore, this is not a graph of a function.


 


 

Problems 15a - 15b:  Determine if the given function is even, odd or neither.

 
15a. 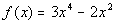problem 15a
 
checkAnswer:

answer 15a1

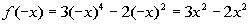
Since 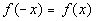answer 15a2, then it is an even function.

 


 

15b. 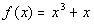problem 15b
 
checkAnswer:

answer 15ba1

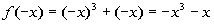
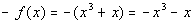
answer 15b2

Since 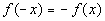answer 15b3, then it is an odd function.


 


 

Problem 16a: If f(x) = int(x), find the given functional value.

 
16a.  f(-14.321)
 
checkAnswer:

-15 is the greatest integer that is less than or equal to -14.321. 
 

buffalo top

 
WTAMU > Virtual Math Lab > College Algebra > Tutorial 33: Practice Test on Tutorials 25 - 32


Last revised on July 3, 2010 by Kim Seward.
All contents copyright (C) 2002 - 2010, WTAMU and Kim Seward. All rights reserved.