College Algebra Tutorial 30
College Algebra
Answer/Discussion to Practice Problems
Tutorial 30B: Operations with Functions
 Answer/Discussion
to 1a
Answer/Discussion
to 1a
*Add the 2 functions
 Answer/Discussion
to 1b
Answer/Discussion
to 1b
*Use the sum found in 1a to plug
in 3 for x
 Answer/Discussion
to 1c
Answer/Discussion
to 1c
*Take the difference of the 2
functions
*Subtract EVERY term of the 2nd
(
)
 Answer/Discussion
to 1d
Answer/Discussion
to 1d
*Multiply the 2 functions
 Answer/Discussion
to 1e
Answer/Discussion
to 1e
*Use the product found in 1d to
plug in -1
for x
 Answer/Discussion
to 1f
Answer/Discussion
to 1f*Write as a quotient of the 2
functions
 Answer/Discussion
to 1g
Answer/Discussion
to 1g
*g is
inside of f
*Substitute 3x - 1 for g
*Plug in 3x -
1 for x in function f
 Answer/Discussion
to 1h
Answer/Discussion
to 1h
*Use the composite function found
in 1g to
plug in 1 for x
 Answer/Discussion
to 1i
Answer/Discussion
to 1i
*f is inside of g
*Substitute x squared
+ 3 for f
*Plug in x squared
+ 3 for x in function g
 Answer/Discussion
to 2a
f = {(1, 2), (2, 3), (3, 4), (4,
5)},
Answer/Discussion
to 2a
f = {(1, 2), (2, 3), (3, 4), (4,
5)},
g = {(1, -2), (3,
-3), (5, -5)}, and
h = {(1, 0), (2,
1), (3, 2)}
When you are looking
for the domain of the sum of two functions that are given as sets, you
are looking for the intersection of their domains.
Since the x values
that f and g have in common are 1 and 3,
then the domain would be {1, 3}.
x = 1:
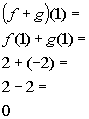 (1, 0)
(1, 0)
*Add together the corresponding y values to x = 1
x = 3:
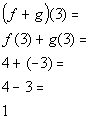 (3, 1)
(3, 1)
*Add together the corresponding y values to x = 3
Putting it together in
ordered pairs we get:
f + g = {(1, 0), (3, 1)}
 Answer/Discussion
to 2b
f = {(1, 2), (2, 3), (3, 4), (4,
5)},
Answer/Discussion
to 2b
f = {(1, 2), (2, 3), (3, 4), (4,
5)},
g = {(1, -2), (3,
-3), (5, -5)}, and
h = {(1, 0), (2,
1), (3, 2)}
When
you are looking for the domain of the difference of two functions that
are
given as sets, you are looking for the intersection of their domains.
Since the x values
that f and g have in common are 1 and 3,
then the domain would be {1, 3}.
x = 1:
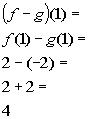 (1, 4)
(1, 4)
*Subtract the corresponding y values to x = 1
x = 3:
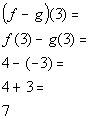 (3, 7)
(3, 7)
*Subtract the corresponding y values to x = 3
Putting it together in
ordered pairs we get:
f - g = {(1, 4), (3, 7)}
 Answer/Discussion
to 2c
f = {(1, 2), (2, 3), (3, 4), (4,
5)},
Answer/Discussion
to 2c
f = {(1, 2), (2, 3), (3, 4), (4,
5)},
g = {(1, -2), (3,
-3), (5, -5)}, and
h = {(1, 0), (2,
1), (3, 2)}
When
you are looking for the domain of the product of two functions that are
given as sets, you are looking for the intersection of their domains.
Since the x values
that f and g have in common are 1 and 3,
then the domain would be {1, 3}.
x = 1:
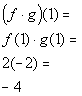 (1, -4)
(1, -4)
*Multiply the corresponding y values to x = 1
x = 3:
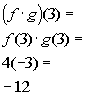 (3, -12)
(3, -12)
*Multiply the corresponding y values to x = 3
Putting it together in
ordered pairs we get:
f g = {(1, - 4), (3, -12)}
 Answer/Discussion
to 2d
f = {(1, 2), (2, 3), (3, 4), (4,
5)},
Answer/Discussion
to 2d
f = {(1, 2), (2, 3), (3, 4), (4,
5)},
g = {(1, -2), (3,
-3), (5, -5)}, and
h = {(1, 0), (2,
1), (3, 2)}
When
you are looking for the domain of the quotient of two functions that
are
given as sets, you are looking for the intersection of their domains
AND values of x that do NOT cause the denominator to equal 0.
The x values that f and h have in common are 1, 2,
and 3. However, h(1) = 0, which would cause the denominator of
the
quotient to be 0.
So, the domain would be {2, 3}.
x = 2:
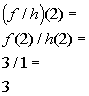 (2, 3)
(2, 3)
*Find the quotient of the
corresponding y values to x = 2
x = 3:
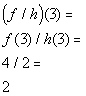 (3, 2)
(3, 2)
*Find the quotient of the
corresponding y values to x = 3
Putting it together in
ordered pairs we get:
f g = {(2, 3), (3, 2)}
 Answer/Discussion
to 2e
f = {(1, 2), (2, 3), (3, 4), (4,
5)},
Answer/Discussion
to 2e
f = {(1, 2), (2, 3), (3, 4), (4,
5)},
g = {(1, -2), (3,
-3), (5, -5)}, and
h = {(1, 0), (2,
1), (3, 2)}
When
you are looking for the domain of the composition of functions that
are
given as sets, you are looking for values that come from the domain of
the inside function AND when you plug those values of x into the inside function, the output is in the domain of the outside
function and so forth.
The x values of h are 1, 2, and 3.
However, g(f(h(1))) =g( f(0)), where f(0) is undefined. Also g(f(h(2))) =g( f(1)) = g(2), where g(2) is
undefined.
So, the domain would be {3}.
x = 3:
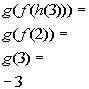 (3, -3)
(3, -3)
*h(3) = 2
*f(2) = 3
*Find the y value that
corresponds to x =
3
Putting it together in
an ordered pair we get:
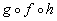
= {(3, -3)}
 Answer/Discussion
to 3a
Answer/Discussion
to 3a
When you are writing a
composition function keep in mind that one function is inside of the
other. You just have to figure out which function is the inside
function and which is the outside function.
Note that if you put g inside of f you
would get:
*Put g inside of f
Hey this looks familiar.
Our answer is 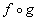 .
.

Last revised on March 31, 2010 by Kim Seward.
All contents copyright (C) 2002 - 2010, WTAMU and Kim Seward. All rights reserved.


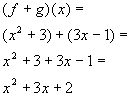
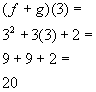
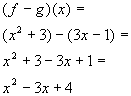
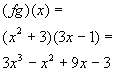
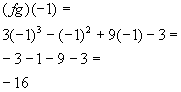
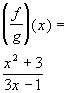
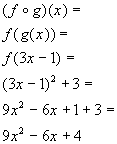
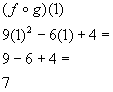
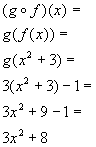
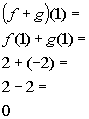
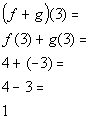
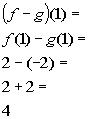
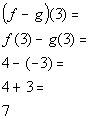
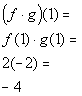
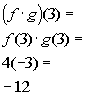
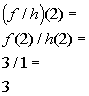
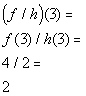
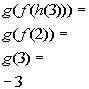
 = {(3, -3)}
= {(3, -3)}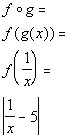
 .
.