College Algebra
Answer/Discussion to Practice Problems
Tutorial 30: Introduction to Functions
 Answer/Discussion
to 1a
{(1, 5), (2, 6), (3, 7), (4, 8)} |
Is this a function or not?
We need to ask ourselves, does every first element
(or input) correspond with EXACTLY ONE second element (or output)?
In this case, the answer is yes. 1 only goes with 5, 2 only goes
with 6, 3 only goes with 7, and 4 only goes with 8.
So, this relation would be an example of a
function.
Domain
We need to find the set of all input values. In terms of ordered
pairs, that correlates with the first component of each one. So,
what do you get for the domain?
If you got {1, 2, 3, 4}, you are correct!
Range
We need to find the set of all output values. In terms of ordered
pairs, that correlates with the second component of each one. SO,
what do you get for the range?
If you got {5, 6, 7, 8}, you are absolutely right! |
Answer/Discussion
to 1b
{(-1, 2), (-1, 3), (2, 4)} |
Is this a function or not?
We need to ask ourselves, does every first element
(or input) correspond with EXACTLY ONE second element (or output)?
In this case, the answer is no. The input value of -1 goes with two
output values, 2 and 3. It only takes one input value to associate
with more than one output value to be invalid as a function.
So, this relation would not be an example of
a function.
Domain
We need to find the set of all input values. In terms of ordered
pairs, that correlates with the first component of each one. So,
what do you get for the domain?
If you got {-1, 2}, you are correct!
Note that if any value repeats, we only need to list it one time.
Range
We need to find the set of all output values. In terms of ordered
pairs, that correlates with the second component of each one. So,
what do you get for the range?
If you got {2, 3, 4}, you are absolutely right! |
Answer/Discussion
to 2a
|
To check if y is a function of x,
we need to solve for y and then check to see
if there is only one output for every input. |
|
*Inverse of add. x squared is sub. x squared
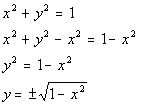
*Inverse of squaring is taking the sq. root
*Solved for y |
At this point we ask ourselves, would we get one value for y if you plug in any value for x?
If you answered no, you are correct.
For example, if our input value x is 0,
then our output value y could either be 1 or -1. Note that
I could have picked an infinite number of examples like this one.
You only need to show one example where the input value is associated with
more than one output value to disqualify it from being a function.
This means that at least one input value is associated with more
than one output value, so by definition, y is not a function of x. |
Answer/Discussion
to 2b
|
To check if y is a function of x,
we need to solve for y first and then check
to see if there is only one output for every input. |
|
*Inverse of add. 2x is
sub. 2x
*Solved for y
|
At this point we ask ourselves, would we get one value for y if you plug in any value for x?
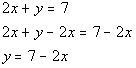
If you answered yes, you are right on. For example, if we plugged in
a 1 for x, then y would only equal one value, 5. Note that ANY value you would plug
in for x would produce only one value for y.
Note that since it is solved for y, y is
our output value and x is our input value.
Since our answer to that question is yes, that means by definition, y is a function of x. |
Answer/Discussion
to 3a
|
Again, think of functional notation as a fancy assignment statement.
For example, when we are looking for f(0),
we are going to plug in 0 for the value of x in
our function f and so forth. |
|
*Plug in -5 for x and evaluate
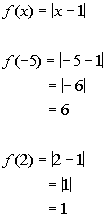
*Plug in 2 for x and evaluate
|
So our answers are f(-5) = 6 and f(2)
= 1. |
Answer/Discussion
to 4a
|
f(a):
Don't let the fact that we need to plug in an a throw you. You plug it into the function just like you do a number.
Everywhere you have an x in your function,
replace it with an a. |
f(a + h)
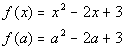
Don't let the fact that we need to plug in the expression a + h throw you. You plug it into the function
just like you do a number. Everywhere you have an x in your function, replace it with an a + h. |
|
*Plug in a + h for x and evaluate
|
 :
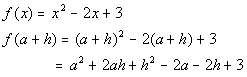
Putting it all together we get: |
|
*Plug in f( a + h) and f(a)
found above
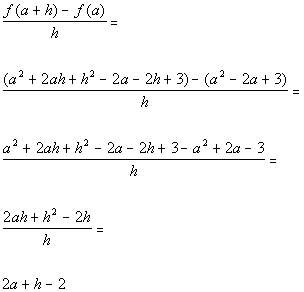
*Combine like terms
*Divide out h from
every term
|
Answer/Discussion
to 5a
|
To find g(-1), we need to go to
the piece of the function that x = -1 would
be under, which would be the first one where x< 0. |
|
*This piece of the function is used when x < 0
*This is a constant function, it is always
equal to 7 |
To find g(0), we need to go to the
piece of the function that x = 0 would be under,
which would be the first one where x < 0. |
|
*This piece of the function is used when x < 0
*This is a constant function, it is always
equal to 7 |
To find g(4), we need to go to the
piece of the function that x = 4 would be under,
which would be the last one where x > 0. |
|
*This piece of the function is used when x > 0
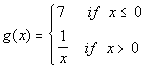
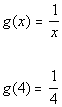
*Plug in 4 for x
|
Answer/Discussion
to 6a
|
Since we can plug in any value for x (input
variable) and get a real number answer for our function (output variable),
then there are no restrictions. Therefore the domain is all real
numbers. |
Answer/Discussion
to 6b
|
Our restriction here is that the denominator of a fraction can never
be equal to 0. So to find our domain, we want to set the denominator
equal to 0 and restrict those values. |
|
*The den. cannot equal to 0
*Factoring to help "solve"
*3 and -1 are restricted values |
Our domain would be all real numbers except 3 and -1, because
3 and -1 both make the denominator equal to 0, which would not give us
a real number answer for our function. |
Answer/Discussion
to 6c
|
This time we do have a restriction on our domain. We can only
take the square root of a number greater than or equal to 0. So we must
set the radicand (the inside of the radical) greater than or equal to 0. |
|
*Inv. of add. 1 is sub. 1
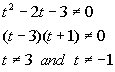
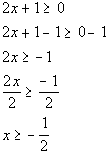
*Inv. of mult. 2 is div. 2
*This is our domain |
Only values of x that are greater than
or equal to -1/2 make the original radicand greater than or equal to 0, so
x > -1/2 is our domain for this
function. |
Last revised on March 29, 2010 by Kim Seward.
All contents copyright (C) 2002 - 2010, WTAMU and Kim Seward. All rights reserved.
|
|
