College Algebra
Answer/Discussion to Practice Problems
Tutorial 27: Graphing Lines
 Answer/Discussion
to 1a
|
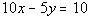
Solve for y to get it into the slope/intercept
form: |
|
*Inverse of add. 10x is sub. 10x
*Inverse of mult. -5 is div. -5
*Slope/intercept form
|
Lining up the form with the equation we got, can you see what the slope
and y-intercept are?
In this form, the slope is m, which
is the number in front of x. In our problem
that would have to be 2.
In this form, the y-intercept is b,
which is the constant. In our problem that would be -2.
How did you do? |
Since the y-intercept is where the line
crosses the y-axis, then x's
value would have to be 0. In step 1 we found our y-intercept
value to be -2.
Putting that together, the ordered pair for the y-intercept
would be (0, -2): |
In step 1 we found our slope to be 2.
Since we have a positive slope the rise and the run need to either be
BOTH positive or BOTH negative. So, we can either rise up 2 and run
right 1 OR go down 2 and left 2.
I chose to rise up 2 and run right 1, starting on the y-intercept: |
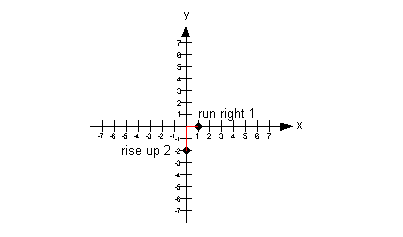
Note that if we would have gone down 2 and left 1 from our y-intercept,
that we would have ended up at (-1, -4) which would have lined up with
the other points. |
Answer/Discussion
to 1b
|
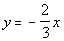
This equation is already in slope/intercept form: |
Lining up the form with the equation we got, can you see what the slope
and y-intercept are?
In this form, the slope is m, which
is the number in front of x. In our problem
that would have to be -2/3.
In this form, the y-intercept is b,
which is the constant. In our problem that would be 0.
How did you do? |
Since the y-intercept is where the line
crosses the y-axis, then x's
value would have to be 0. In step 1 we found our y-intercept
value to be 0.
Putting that together, the ordered pair for the y-intercept
would be (0, 0): |
In step 1 we found our slope to be -2/3.
Since we have a negative slope the rise and the run have to be opposites
of each other, one has to be positive and one has to be negative.
So, we can either go down 2 and run right 3 OR rise up 2 and run left 3.
I chose to go down 2 and run right 3, starting on the y-intercept: |
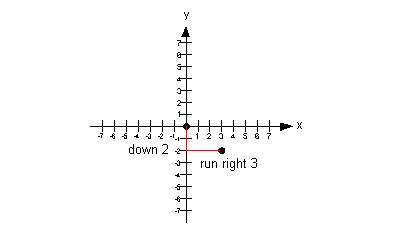
Note that if we would have rose up 2 and ran left 3 from our y-intercept,
that we would have ended up at (-3, 2) which would have lined up with the
other points. |
Answer/Discussion
to 1c
|
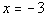
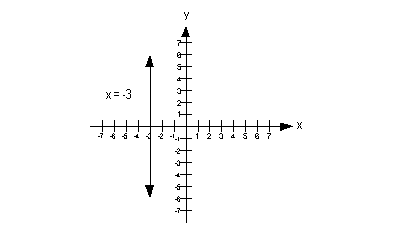
Since we have a vertical line, what is our slope going to be?
If you said undefined, you are so right!!!
What would the y-intercept be? Give
yourself a high five if you said there is no y-intercept. |
Answer/Discussion
to 1d
|
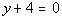
Note how we are missing an x and even though
it is not quite in the form y = c,
that we can get it in that form.
Lets first rewrite this in the form y = c and then go from there: |
|
*Written in the form y = c |
Note how we have an equation that has y set equal to a constant, where there is no x.
Since this fits the
form of y = c described
above, we can jump to the chase and draw our horizontal line: |
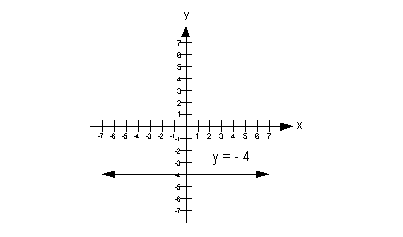
Since we have a horizontal line, what is our slope going to be?
If you said 0, you are so right!!!
What would the y-intercept be? Give
yourself a high five if you said -4. |
Last revised on Feb. 11, 2010 by Kim Seward.
All contents copyright (C) 2002 - 2010, WTAMU and Kim Seward. All rights reserved.
|
|
)
and identify the slope and y-intercept.
