

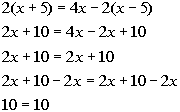
Since the variable dropped out AND it is a true statement, the answer is all real numbers, which means this equation is an identity.
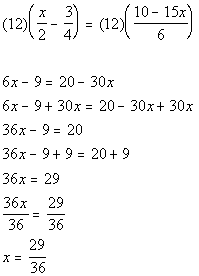
Since we came up with the solution x = 29/36, this would be an example of a conditional equation.
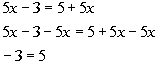
Since the variable dropped out AND it is a false statement, the answer is no solution which means this is an inconsistent equation.
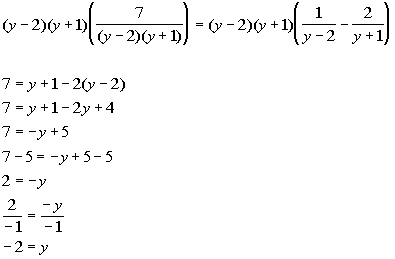
Note that -2 does not cause any denominators to be zero. So it is not an extraneous solution.
-2 is the solution to our equation.
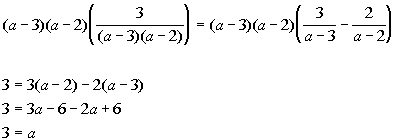
Note that 3 does cause two of the denominators to be zero.
So 3 is an extraneous solution. That means there is no solution.
The answer is NO solution.
Since their sum is 30, we
get the following
equation:
![]()
Solving the equation we get:
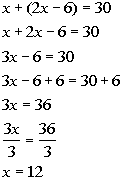
Answer:
Tommy scored 12 points.
Ralph scored 2(12) - 6 = 18 points.
Since the sum of the 1st,
four times the 2nd,
and twice the 3rd is 86, we get the following equation:
![]()
Solving the equation we get:
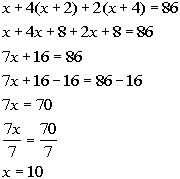
Answer:
The three ages are 10, 12, and 14.
Since the markdown price
is $960, we get the
following equation:
![]()
Solving the equation we get:
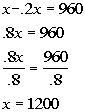
Answer:
The original price of the computer is $1200.
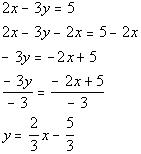
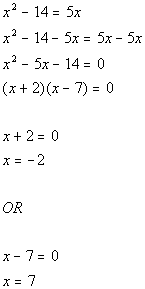
There are two solutions to this equation: x = -2 and x = 7.
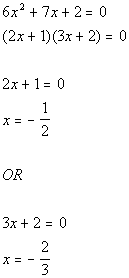
There are two solutions to this equation: x = -1/2 and x = -2/3.
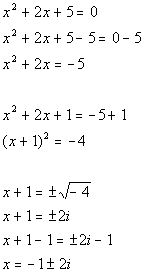
There are two solutions to this equation: x = -1 + 2i and x = -1 - 2i.
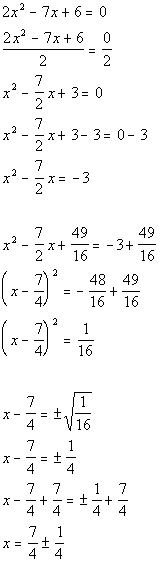
There are two solutions to this equation: x = 7/4 + 1/4 = 2 and x = 7/4 - 1/4 = 6/4 = 3/2 .
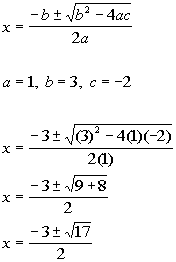
Write in standard form:
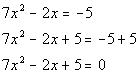
Put in quadratic formula:
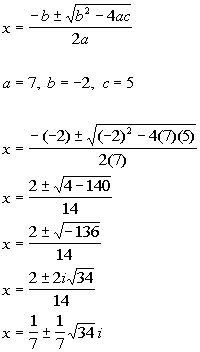
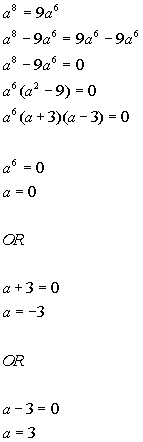
There are three solutions to this equation: a = 0, a = -3, and a = 3.
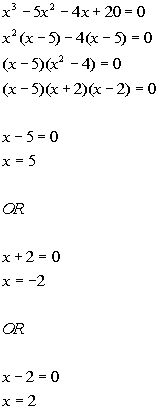
There are three solutions to this equation: x = 5, x = -2, and x = 2.
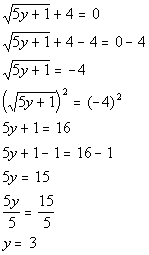
Checking for extraneous solutions:
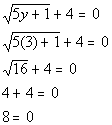
Since we got a false statement, y = 3 is an extraneous solution.
This means there is no solution to this equation.
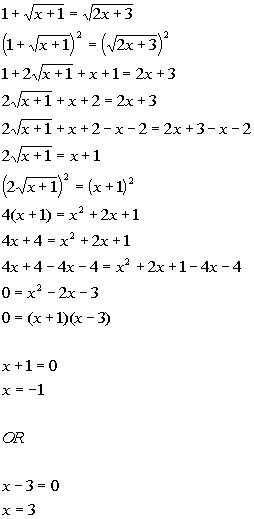
Both x = -1 and x = 3 check.
There are two solutions to this equation: x = -1 and x = 3.
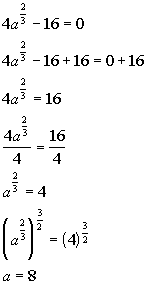
a = 8 does check.
There is one solution to this equation: a = 8.
Writing the equation in standard form:
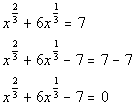
Substitution:
![]()
Substitute in t and
solve:
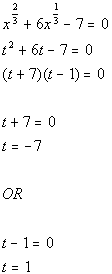
Substitute value in for t and solve for x:
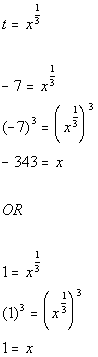
There are two solutions to this equation: x = -343 and x = 1.
Substitution:
![]()
Substitute in t and
solve:
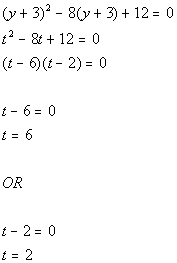
Substitute value in for t and solve for y:
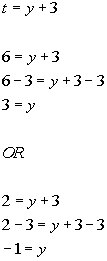
There are two solutions to this equation: y = 3 and y = -1.
First solution:
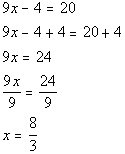
Second solution:
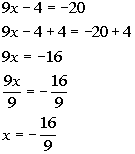
There are two solutions to this equation: x = 8/3 and x = -16/9.
Since the absolute value is set equal to a negative number, there is no solution.
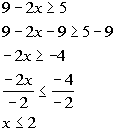
Interval notation: ![]()
Graph:
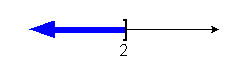
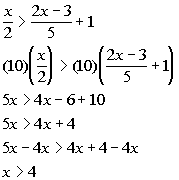
Interval notation: ![]()
Graph:
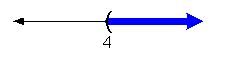
Use the definition of absolute value to set up:
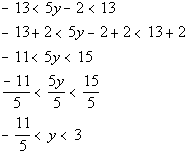
Interval notation: ![]()
Graph:
![]()
Use the definition of absolute value to set up:
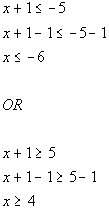
Interval notation: ![]()
Graph:
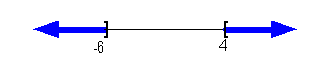
Isolate the absolute
value:
![]()
Since the absolute value is ALWAYS positive and in this problem it is set greater than or equal to a negative number, the answer is all real numbers.
Since the absolute value is ALWAYS positive and in this problem it is set less than a negative number, the answer is no solution.
Write in standard form:
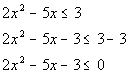
Solve quadratic equation:
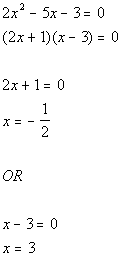
Mark off boundary points on number line:

Note that the two boundary points create three sections on the
graph: ![]() ,
, ![]()
![]() .
.
Chose -1 in first interval to check:
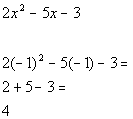
Since 4 is positive and we are looking for values
that cause our quadratic
expression to be less than or equal to 0 (negative or 0), ![]() would
not be part of the solution.
would
not be part of the solution.
Chose 0 in second interval to check:
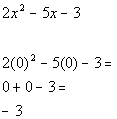
Since -3 is negative and we are looking for values
that cause our expression
to be less than or equal to 0 (negative or 0), ![]() would be part of the solution.
would be part of the solution.
Chose 4 in third interval to check:
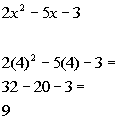
Since 9 is positive and we are looking for values
that cause our quadratic
expression to be less than or equal to 0 (negative or 0), ![]() would
not be part of the solution.
would
not be part of the solution.
Interval notation: ![]()
Graph:
![]()
Set numerator equal to 0 and solve:
![]()
Set denominator equal to 0 and solve:
![]()
Mark off boundary points on number line:

Note that the two boundary points create three sections on the
graph: ![]() ,
, ![]() ,
and
,
and ![]() .
.
Chose -4 in first interval to check:
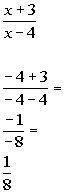
Since 1/8 is positive and we are looking for
values that cause our quadratic
expression to be greater than 0 (positive), ![]() would
be part of the solution.
would
be part of the solution.
Chose 0 in second interval to check:
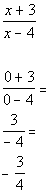
Since -3/4 is negative and we are looking for
values that cause our
quadratic expression to be greater than 0 (positive), ![]() would
not be part of the solution.
would
not be part of the solution.
Chose 5 in third interval to check:
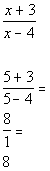
Since 8 is positive and we are looking for values
that cause our quadratic
expression to be greater than 0 (positive), ![]() would
be part of the solution.
would
be part of the solution.
Interval notation: ![]()
Graph:
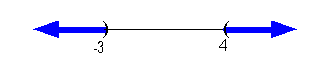
Last revised on Jan. 15, 2010 by Kim Seward.
All contents copyright (C) 2002 - 2010, WTAMU and Kim Seward.
All rights reserved.