College Algebra
Answer/Discussion to Practice Problems
Tutorial 11: Complex Rational Expressions

WTAMU > Virtual Math Lab > College Algebra > Tutorial 11: Complex Rational Expressions

Answer/Discussion to 1a

Step 1: If needed, rewrite the numerator and denominator so that they are each a single fraction.

Combining only the numerator we get:

*Rewrite fractions with LCD of y

Combining only the denominator we get:

*Rewrite fractions with LCD of y

Putting these back into the complex fraction we get:

*Write numerator over denominator

Step 2: Divide the numerator by the denominator

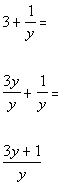
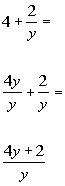
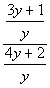
AND

Step 3: If needed, simplify the rational expression.

*Rewrite div. as mult. of reciprocal

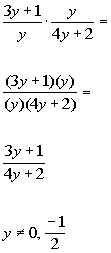
*Divide out a common factor of y

*Excluded values of the original den.

Note that the values that would be excluded from the domain are 0 and -1/2. These are the values that make the original denominators equal to 0.

(return to problem 1a)

Answer/Discussion to 1b

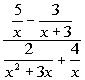
problem 1b

Step 1: Multiply the numerator and denominator of the overall complex fractions by the LCD of the smaller fractions.

The denominators of the numerator's fractions have the following factors:

The denominators of the denominator's fractions have the following factors:

Putting all the different factors together and using the highest exponent, we get the following LCD for all the small fractions:

Multiplying numerator and denominator by the LCD we get:

*Mult. num. and den. by x(x +3)

Step 2: If needed, simplify the rational expression.

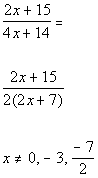
*Factor the GCF of 2
*No common factors to divide out

*Excluded values of the original den.

Note that the values that would be excluded from the domain are 0, -3 and -7/2. These are the values that make the original denominators equal to 0.

(return to problem 1b)

WTAMU > Virtual Math Lab > College Algebra > Tutorial 11: Complex Rational Expressions