Beginning Algebra Tutorial on Simplifying Algebraic Expressions

Beginning Algebra
Tutorial 11:
Simplifying Algebraic Expressions

Learning Objectives

After completing this tutorial, you should be able to:

Identify a term, coefficient, constant term, and like terms.
Combine like terms.
Simplify an expression using distributive property and combining like terms.

Introduction

In this tutorial we will be looking at various components of terms. Then we will move on to adding like terms together. Some of these concepts are based on ideas that were covered in earlier tutorials. Alot of times in math you are using previous knowledge to learn new concepts. The trick is to not reinvent the wheel each time, but recognize what you have done before and draw on that knowledge to help you work through the problems.

Tutorial

Term

A term is a number, variable or the product of a number and variable(s).

Examples of terms are 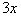, , 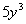, 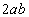z

Coefficient

A coefficient is the numeric factor of your term.

Here are the coefficients of the terms listed above:

Term	Coefficient
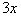
	3
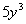
	5
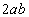
	2
z	1

Constant Term

A constant term is a term that contains only a number. In other words, there is no variable in a constant term.

Examples of constant terms are 4, 100, and -5.

Like Terms

Like terms are terms that have the exact same variables raised to the exact same exponents.

One example of like terms is 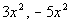. Another example is .

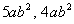Combining Like Terms

You can only combine terms that are like terms. You think of it as the reverse of the distributive property.

It is like counting apples and oranges. You just count up how many variables you have the same and write the number in front of the common variable part.

Example 1: Simplify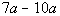

by combining like terms.

Are there any like terms that we can combine?

It looks like it. Both terms have the same variable part, a.

*Use distributive prop. to combine like terms

Example 2: Simplify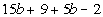

by combining like terms.

Are there any like terms that we can combine?

It looks like it. Two terms have the same variable part, b. The other pair of terms are constant terms that can be combined together.

*Use distributive prop. to combine like terms

From here on out I will not be showing the distributive property step when combining like terms. I will go right into adding or subtracting the coefficients of the like terms. I showed you the distributive property in the above examples to give you the thought behind combining like terms.

Example 3: Simplify the expression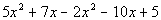

It looks like we have two terms that have an x squared that we can combine and we have two terms that have an x that we can combine. The poor 5 does not have anything it can combine with so it will have to stay 5.

Grouping like terms together and combining them we get:

*Combine the x squared terms together
and then the x terms together

Example 4: Simplify the expression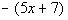

*A - outside a ( ) is the same as times (-1)
*Distribute the (-1) to EVERY term inside ( )
*Multiply

Basically, when you have a negative sign in front of a ( ), like this example, you can think of it as taking a -1 times the ( ). What you end up doing in the end is taking the opposite of every term in the ( ).

Example 5: Simplify the expression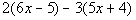

Let's first apply the distributive property (found in Tutorial 8: Properties of Real Numbers) and see what we get:

*Dist. 2 to EVERY term of 1st ( )
*Dist. -3 to EVERY term of 2nd ( )
*Multiply

Regrouping and combining like terms we get:

*x is distributed to the 1st 2 terms
*Reverse Dist. Prop with x
*Subtract

Example 6: Write the following as an algebraic expression and simplify if possible.

Add 3a + 9 to 7a - 2.

Basically we will be adding these two expressions together.

Writing this as an algebraic expression we get:

Regrouping and combining like terms we get:

Example 7: Write the following as an algebraic expression and simplify if possible.

The sum of 5 times a number and 2, subtracted from 12 times a number.

x is representing the unknown number. The sum of 5 times a number and 2 can be written as 5x + 2. From there we need to subtract that from 12x.

Writing this as an algebraic expression we get:

Using the distributive property (found in Tutorial 8: Properties of Real Numbers) and then combining like terms we get:

Practice Problems

These are practice problems to help bring you to the next level. It will allow you to check and see if you have an understanding of these types of problems. Math works just like anything else, if you want to get good at it, then you need to practice it. Even the best athletes and musicians had help along the way and lots of practice, practice, practice, to get good at their sport or instrument. In fact there is no such thing as too much practice.

To get the most out of these, you should work the problem out on your own and then check your answer by clicking on the link for the answer/discussion for that problem. At the link you will find the answer as well as any steps that went into finding that answer.

Practice Problem 1a:

Simplify by combining like terms.

1a.

(answer/discussion to 1a)

Practice Problems 2a - 2b:

Simplify the expressions.

2a.

(answer/discussion to 2a)

2b.

(answer/discussion to 2b)

Practice Problem 3a:

Write the following as an algebraic expression and simplify if possible.

3a. The sum of 9 times a number and 5, subtracted from 4 times a number.
(answer/discussion to 3a)

Need Extra Help on These Topics?

The following are webpages that can assist you in the topics that were covered on this page:

http://www.math.com/school/subject2/lessons/S2U2L4DP.html
This webpage goes over what like terms are.

http://www.purplemath.com/modules/polydefs.htm#Combining
This webpage goes over combining like terms.

http://www.mathleague.com/help/algebra/algebra.htm#combiningliketerms
This webpage goes over combining like terms.

Go to Get Help Outside the Classroom found in Tutorial 1: How to Succeed in a Math Class for some more suggestions.

(Back to the Beginning Algebra Homepage)

(Back to the GRE Math Help Page)